题目内容
【题目】已知椭圆![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在圆心在原点的定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
【答案】(1)![]() (2)存在;定圆
(2)存在;定圆![]()
【解析】
(1)根据椭圆的离心率和椭圆经过的点的坐标,代入椭圆方程中,求出a、b,即可得到椭圆C的方程.
(2)根据条件,分直线![]() 的斜率不存在和直线的斜率不存在两种情况分别求出定圆的方程,,当直线
的斜率不存在和直线的斜率不存在两种情况分别求出定圆的方程,,当直线![]() 的斜率存在时,设直线方程为
的斜率存在时,设直线方程为![]() ,联立方程组,令
,联立方程组,令![]() ,,利用韦达定理,结合
,,利用韦达定理,结合![]() .推出
.推出![]() ,利用直线
,利用直线![]() 与圆相切,求出圆的半径,得到圆的方程,即可得到结果.
与圆相切,求出圆的半径,得到圆的方程,即可得到结果.
解:(1)椭圆![]() 经过点
经过点![]() ,∴
,∴![]() ,又∵
,又∵![]() ,解之得
,解之得![]() ,
,![]() .
.
所以椭圆![]() 的方程为
的方程为![]() ;
;
(2)当直线![]() 的斜率不存在时,由对称性,设
的斜率不存在时,由对称性,设![]() ,
,![]() .
.
∵![]() ,
,![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,∴
,∴![]() .
.
∴![]() 到直线
到直线![]() 的距离为
的距离为![]() ,所以
,所以![]() .
.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() ,
,
由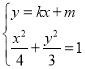 得
得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
故存在定圆![]() 与直线
与直线![]() 总相切.
总相切.

【题目】心理学家发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学,给所有同学几何和代数各一题,让各位同学自由选择一道题进行解答,统计情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男 同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)现从选择几何题的8名女生中任意抽取两人对他们的答题进行研究,记甲、乙两名女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
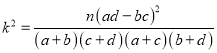
【题目】已知甲、乙两名工人在同样条件下每天各生产100件产品,且每生产1件正品可获利20元,生产1件次品损失30元,甲,乙两名工人100天中出现次品件数的情况如表所示.
甲每天生产的次品数/件 | 0 | 1 | 2 | 3 | 4 |
对应的天数/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生产的次品数/件 | 0 | 1 | 2 | 3 |
对应的天数/天 | 30 | 25 | 25 | 20 |
(1)将甲每天生产的次品数记为![]() (单位:件),日利润记为
(单位:件),日利润记为![]() (单位:元),写出
(单位:元),写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如果将统计的100天中产生次品量的频率作为概率,记![]() 表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量
表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.