题目内容
2.已知数列{an}满足an=n•($\frac{9}{10}$)n-1,n∈N*,如何求数列{an}中的最大项,最小项是多少?分析 由$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{(n+1)•(\frac{9}{10})^{n}}{n•(\frac{9}{10})^{n-1}}$=$\frac{9n+9}{10n}$=$\frac{9}{10}+\frac{9}{10n}$,可知:$\frac{9}{10}+\frac{9}{10n}$(n∈N*)是关于n的单调递减数列,对n分类讨论即可得出.
解答 解:由$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{(n+1)•(\frac{9}{10})^{n}}{n•(\frac{9}{10})^{n-1}}$=$\frac{9n+9}{10n}$=$\frac{9}{10}+\frac{9}{10n}$,
可知:$\frac{9}{10}+\frac{9}{10n}$(n∈N*)是关于n的单调递减数列,
并且当n<9时,$\frac{{a}_{n+1}}{{a}_{n}}$>1,即an<an+1;
当n=9时,$\frac{{a}_{n+1}}{{a}_{n}}$=1,即a9=a10;
当n>9时,$\frac{{a}_{n+1}}{{a}_{n}}$<1,即an>an+1.
综上可得:a1<a2<…<a9=a10>a11>….
∴数列{an}中的最大项是a9,a10,
最小项与n有关系.
点评 本题考查了数列的单调性、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.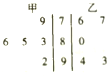 将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:
将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:
①甲生的平均成绩大于乙生的平均成绩;
②甲生的平均成绩小于乙生的平均成绩;
③甲生成绩的方差大于乙生成绩的方差;
④甲生成绩的方差小于乙生成绩的方差.
其中根据茎叶图能得到正确的统计结论的编号为( )
 将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:
将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:①甲生的平均成绩大于乙生的平均成绩;
②甲生的平均成绩小于乙生的平均成绩;
③甲生成绩的方差大于乙生成绩的方差;
④甲生成绩的方差小于乙生成绩的方差.
其中根据茎叶图能得到正确的统计结论的编号为( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
14.数列{an}的通项公式an=-58+16n-n2,则( )
| A. | {an}是递增数列 | B. | {an}是递减数列 | ||
| C. | {an}先增后减,有最大值 | D. | {an}先减后增,有最小值 |
2.函数f(x)=lg($\frac{1}{\sqrt{{x}^{2}+1}+x}$)的奇偶性是( )
| A. | 奇函数 | B. | 偶函数 | C. | 既奇又偶函数 | D. | 非奇非偶函数 |