题目内容
中心在原点，焦点在
轴上的双曲线
的离心率为
，直线与双曲线交于
两点，线段
中点
在第一象限，并且在抛物线
上，且到抛物线焦点的距离为
，则直线的斜率为（ ）
A． | B． | C． | D． |
D
解析试题分析：∵到抛物线焦点的距离为，∴
，∴M
，设点
,代入双曲线方程
相减得
，又双曲线的离心率为，∴
，∴
，∴
，故选D
考点：本题考查了直线与双曲线的位置关系
点评：熟练掌握双曲线中的“中点弦”问题是解决此类问题的关键，属基础题
练习册系列答案
名师金手指领衔课时系列答案
相关题目
为抛物线
上一个动点，直线
：
，
：
，则
直线
与曲线
的交点个数为（ ）
| A．4个 | B．1个 | C．2个 | D．3个 |
已知双曲线
的一个焦点与抛物线
的焦点重合，且双曲线的离心率等于
，则该双曲线的方程为( )
A． | B． | C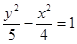． | D． |
抛物线
的焦点F是椭圆
的一个焦点，且它们的交点M到F的距离为
，则椭圆的离心率为
A． | B． | C． | D． |
等轴双曲线
的中心在原点，焦点在
轴上，与抛物线
的准线交于
两点，
，则的实轴长为（ ）
A． | B． | C． | D． |
如图，
是平面
的斜线段，
为斜足。若点
在平面内运动，使得
的面积为定值，则动点的轨迹是（ ）
| A．圆 | B．椭圆 |
| C．一条直线 | D．两条平行直线 |
已知抛物线Cl:y2= 2x的焦点为F1，抛物线C2:y=2x2的焦点为F2，则过F1且与F1F2垂直的直线
的一般方程式为
| A．2x－ y－l=0 | B．2x+ y－1=0 |
| C．4x－y－2 =0 | D．4x－3y－2 =0 |
的一个焦点与抛物线
的焦点重合，且双曲线的离心率等于
，则该双曲线的方程为( )
