题目内容
若（x-1）n的展开式中只有第10项的二项式系数最大，
（1）求展开式中系数最大的项；
（2）设（2x-1）n=a0+a1x+a2x2+…+anxn，求a0+a2+a4+…+an．
（1）求展开式中系数最大的项；
（2）设（2x-1）n=a0+a1x+a2x2+…+anxn，求a0+a2+a4+…+an．
（1）∵（x-1）n的展开式中只有第10项的二项式系数最大，
∴n=18．
设第r+1项的系数最大，则Tr+1=
x18-r•(-1)r，
∴r为偶数，且C
最大，
即r=8或10．
即展开式中系数最大的项为第9项和第11项的系数最大．
∴T10=
x10，T11=
x8．
（2）令x=1，则a0+a1+a2+…+a18=1，
令x=-1，则a0-a1+a2-…+a18=[（a0+a2+a4+…+a18）-（a1+a3+a5+…+a17）]=（-3）18=318，
∴两式相加得：2（a0+a2+a4+…+a18）=318+1．
∴a0+a2+a4+…+a18=
．
故答案为：1．
∴n=18．
设第r+1项的系数最大，则Tr+1=
| C | r18 |
∴r为偶数，且C
| r18 |
即r=8或10．
即展开式中系数最大的项为第9项和第11项的系数最大．
∴T10=
| C | 918 |
| C | 1018 |
（2）令x=1，则a0+a1+a2+…+a18=1，
令x=-1，则a0-a1+a2-…+a18=[（a0+a2+a4+…+a18）-（a1+a3+a5+…+a17）]=（-3）18=318，
∴两式相加得：2（a0+a2+a4+…+a18）=318+1．
∴a0+a2+a4+…+a18=
| 1+318 |
| 2 |
故答案为：1．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
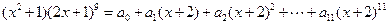，则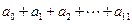
的值为（ ）
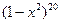展开式中，如果第
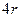项和第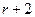
项的二项式系数相等，则
，
.