题目内容
在直角坐标系中,已知点列P1(1,-
),P2(2,
),P3(3,-
),…,Pn(n,(-
)n),…,其中n是正整数.连接P1 P2的直线与x轴交于点X1(x1,0),连接P2 P3的直线与x轴交于点X2(x2,0),…,连接Pn Pn+1的直线与x轴交于点Xn(xn,0),….
(1)求数列{an}的通项公式;
(2)依次记△X1P2X2的面积为S1,△X2P3X3的面积为S3,…,△XnPn+1Xn的面积为Sn,…试求无穷数列{Sn}的各项和.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)依次记△X1P2X2的面积为S1,△X2P3X3的面积为S3,…,△XnPn+1Xn的面积为Sn,…试求无穷数列{Sn}的各项和.
(1)∵Pn(n,(-
)n),Pn+1(n+1,(-
)n+1),
∴直线PnPn+1的方程为:
=
=(-
) (-
)n,
∴令y=0,得-(-
)n=(-
) (-
)n(x-n),
整理,得x-n=
,
∴xn=x=n+
.
即xn=n+
,n∈N*.
(2)由题设条件能够导出Sn=
,
∴数列{an}是首项为
,公比为
的等比数列,
∴S=
Sn=
=
.
| 1 |
| 2 |
| 1 |
| 2 |
∴直线PnPn+1的方程为:
y-(-
| ||
| x-n |
(-
| ||||
| (n+1)-n |
| 3 |
| 2 |
| 1 |
| 2 |
∴令y=0,得-(-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
整理,得x-n=
| 2 |
| 3 |
∴xn=x=n+
| 2 |
| 3 |
即xn=n+
| 2 |
| 3 |
(2)由题设条件能够导出Sn=
| 1 |
| 2n+2 |
∴数列{an}是首项为
| 1 |
| 8 |
| 1 |
| 2 |
∴S=
| lim |
| n→∞ |
| ||
1-
|
| 1 |
| 4 |

练习册系列答案
相关题目
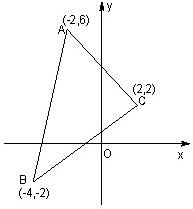 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: