题目内容
 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:| 3 |
| AP |
| PB |
分析:设出A,B的坐标,分别代入两条直线方程,求出向量
,
的坐标,结合
=2
列式,最后把所有量都用x2表示,代入两点求斜率公式得答案.
| AP |
| PB |
| AP |
| PB |
解答:解:设A(x1,y1),B(x2,y2),
则y1=x1,y2=-
x2 ①.
又点P(a,0)(a>0),
则
=(a-x1,-y1),
=(x2-a,y2),
由
=2
,得
②.
联立①②得:a=(
+2)x2.
∴直线l的斜率k=
=
=
=3(2+
).
故答案为:3(2+
).
则y1=x1,y2=-
| ||
| 3 |
又点P(a,0)(a>0),
则
| AP |
| PB |
由
| AP |
| PB |
|
联立①②得:a=(
2
| ||
| 3 |
∴直线l的斜率k=
| y2-y1 |
| x2-x1 |
| 3y2 |
| x2+2x2-a |
=
-
| ||||
3x2-(
|
| 3 |
故答案为:3(2+
| 3 |
点评:本题考查了平行向量与共线向量,考查了两点求直线的斜率,体现了整体运算思想方法,考查了学生的计算能力,是中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
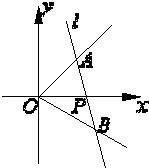 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB: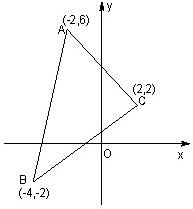 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,直线y=6-x与
如图,在直角坐标系中,直线y=6-x与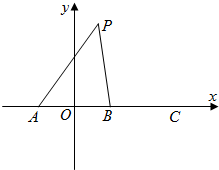 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.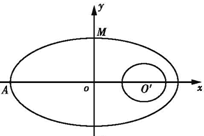 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为