题目内容
在直角坐标系中，已知A（cosx，sinx），B=（1，1），O为坐标原点，
+
=
，f（x）=|
|2．
（Ⅰ）求f（x）的对称中心的坐标及其在区间[-π，0]上的单调递减区间；
（Ⅱ）若f（x0）=3+
，x0∈[
，
]，求tanx0的值．
| OA |
| OB |
| OC |
| OC |
（Ⅰ）求f（x）的对称中心的坐标及其在区间[-π，0]上的单调递减区间；
（Ⅱ）若f（x0）=3+
| 2 |
| π |
| 2 |
| 3π |
| 4 |
分析：（Ⅰ）先利用向量知识，求得f（x）的解析式，再求f（x）的对称中心的坐标及其在区间[-π，0]上的单调递减区间；
（Ⅱ）利用f（x0）=3+
，x0∈[
，
]，求得x0的值，再求tanx0的值．
（Ⅱ）利用f（x0）=3+
| 2 |
| π |
| 2 |
| 3π |
| 4 |
解答：解：（Ⅰ）∵A（cosx，sinx），B=（1，1），
∴
=（cosx，sinx），
=（1，1），
∴
=
+
=（1+cosx，1+sinx）…（2分）
∴f（x）=|
|2=（1+cosx）2+（1+sinx）2=3+2（sinx+cosx）=3+2
sin（x+
）…（4分）
由x+
=kπ，k∈Z，即x=kπ-
，∴对称中心是（kπ-
，3），k∈Z
当2kπ+
≤x+
≤2kπ+
时，f（x）单调递减，即2kπ+
≤x≤2kπ+
，k∈Z
∴f（x）的单调递减区间是[2kπ+
，2kπ+
]，k∈Z…（6分）
∴f（x）在区间[-π，0]上的单调递减区间为[-π，-
]．…（8分）
（Ⅱ）∵f（x0）=3+2
sin（x0+
）=3+
，
∴sin（x0+
）=
∵x0∈[
，
]，∴x0+
=
，∴x0=
∴tanx0=tan
=tan（
+
）=-2-
．…（12分）
∴
| OA |
| OB |
∴
| OC |
| OA |
| OB |
∴f（x）=|
| OC |
| 2 |
| π |
| 4 |
由x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
当2kπ+
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
∴f（x）的单调递减区间是[2kπ+
| π |
| 4 |
| 5π |
| 4 |
∴f（x）在区间[-π，0]上的单调递减区间为[-π，-
| 3π |
| 4 |
（Ⅱ）∵f（x0）=3+2
| 2 |
| π |
| 4 |
| 2 |
∴sin（x0+
| π |
| 4 |
| 1 |
| 2 |
∵x0∈[
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
| 5π |
| 6 |
| 7π |
| 12 |
∴tanx0=tan
| 7π |
| 12 |
| π |
| 3 |
| π |
| 4 |
| 3 |
点评：本题考查向量知识的运用，考查三角函数的学生，解题的关键是确定函数的解析式，属于中档题．
练习册系列答案
优等生题库系列答案
相关题目
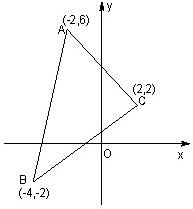如图，在直角坐标系中，已知△ABC的三个顶点的坐标，求：
如图，在直角坐标系中，已知射线OA：x-y=0（x≥0），OB：