题目内容
在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:x+
y=0(x≥0),过点P(1,0)作直线分别交射线OA,OB于A,B点.
(1)当AB中点为P时,求直线AB的方程;
(2)在(1)的条件下,若A、B两点到直线l:y=mx+2的距离相等,求实数m的值.
| 3 |
(1)当AB中点为P时,求直线AB的方程;
(2)在(1)的条件下,若A、B两点到直线l:y=mx+2的距离相等,求实数m的值.
分析:(1)根据A在射线OA上,设A(a,a),根据P为线段AB中点,利用中点坐标公式变形出B坐标,代入射线OB解析式求出a的值,确定出A与B坐标,即可求出直线AB解析式;
(2)法1:若A、B两点到直线l:y=mx+2的距离相等,得到直线l与直线AB平行或过A、B中点,根据直线AB的斜率求出m的值,根据线段AB中点坐标求出m的值即可;
法2:利用点到直线的距离公式列出方程,求出方程的解即可得到m的值.
(2)法1:若A、B两点到直线l:y=mx+2的距离相等,得到直线l与直线AB平行或过A、B中点,根据直线AB的斜率求出m的值,根据线段AB中点坐标求出m的值即可;
法2:利用点到直线的距离公式列出方程,求出方程的解即可得到m的值.
解答:解:(1)设A(a,a),
∵A、B的中点为P,
∴B(2-a,-a),
将B代入射线OB解析式得:
×(2-a)+3×(-a)=0,
解得:a=
-1,
∴A(
-1,
-1),B(3-
,1-
),
则直线AB为y=(-1-
)(x-1);
(2)法1:若A、B两点到直线l:y=mx+2的距离相等,
∴直线l与直线AB平行或过A、B中点,
∵直线AB斜率为-1-
,线段AB中点坐标为(1,0),
∴m=-1-
或m=-2;
法2:由A、B两点到l:mx-y+2=0距离相等
得
=
,
∴m=-1-
或m=-2.
∵A、B的中点为P,
∴B(2-a,-a),
将B代入射线OB解析式得:
| 3 |
解得:a=
| 3 |
∴A(
| 3 |
| 3 |
| 3 |
| 3 |
则直线AB为y=(-1-
| 3 |
(2)法1:若A、B两点到直线l:y=mx+2的距离相等,
∴直线l与直线AB平行或过A、B中点,
∵直线AB斜率为-1-
| 3 |
∴m=-1-
| 3 |
法2:由A、B两点到l:mx-y+2=0距离相等
得
|m(
| ||||
|
|m(3-
| ||||
|
∴m=-1-
| 3 |
点评:此题考查了点到直线的距离公式,线段中点坐标公式,以及两直线的交点坐标,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
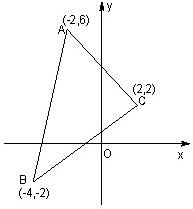 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: