题目内容
13. 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:| x | -1 | 0 | 4 | 5 |
| f(x) | -1 | -2 | -2 | -1 |
②函数f(x)在[2,4]上是减函数;
③如果当x∈[m,5]时,f(x)的最小值是-2,那么m的最大值为4;
④函数y=f(x)-a(a∈R)的零点个数可能为0、1、2、3、4个.
其中正确命题的是①②③④.
分析 先由导函数的图象和原函数的关系画出原函数的大致图象,再借助与图象和导函数的图象,对4个命题,一一进行验证可得到答案.
解答 解:由导函数的图象和原函数的关系得,原函数的大致图象可由以下两种代表形式,如图: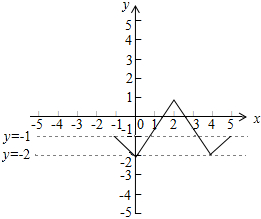
由图得:①由图象可知f′(2)=0,f(x)在x=2处取得极大值,故①正确;
②因为在[2,4]上导函数为负,故原函数递减,故②正确;
③如果当x∈[m,5]时,f(x)的最小值是-2,则m∈[-1,4],即m的最大值为4,故③正确;
④由图可知:
若f(2)=M>-1时,函数的最大值为M,则:
当a>M或a<-2时,函数y=f(x)-a有0个零点;
当a=M时,函数y=f(x)-a有1个零点;
当a=-2或-1<a<M时,函数y=f(x)-a有2个零点;
当-2<a≤-1时,函数y=f(x)-a有4个零点;
若f(2)=M=-1时,函数的最大值为-1,则:
当a>-1或a<-2时,函数y=f(x)-a有0个零点;
当a=-2时,函数y=f(x)-a有2个零点;
当a=-1时,函数y=f(x)-a有3个零点;
当-2<a≤-1时,函数y=f(x)-a有4个零点;
若f(2)=M<-1时,函数的最大值为-1,则:
当a>-1或a<-2时,函数y=f(x)-a有0个零点;
当a=-2或M<a<-1时,函数y=f(x)-a有2个零点;
当a=M时,函数y=f(x)-a有3个零点;
当-2<a<M时,函数y=f(x)-a有4个零点;
故函数y=f(x)-a(a∈R)的零点个数可能为0、1、2、3、4个,故④正确;
综上得:真命题有①②③④.
故答案为:①②③④
点评 本题主要考查导函数和原函数的单调性之间的关系.二者之间的关系是:导函数为正,原函数递增;导函数为负,原函数递减

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知m,n是两条不同的直线,α,β是两个不同的平面,下列判断正确的是( )
| A. | 若m∥α,α∥β,则m∥β | B. | 若m?α,n?α,m∥β,n∥β,则α∥β | ||
| C. | 若m∥n,m⊥α,α∥β,则n⊥β | D. | 若m?α,α⊥β,则m⊥β |
18.已知直线x-2y+4=0经过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的顶点和焦点,则椭圆的标准方程为( )
| A. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1 |