题目内容
5.已知抛物线关于x轴对称,顶点在坐标原点,并且经过点$M(2,-2\sqrt{2})$,斜率为1的直线l经过抛物线的焦点,且与抛物线相交于A,B两点.(1)求抛物线的标准方程;
(2)求线段AB的长.
分析 (1)设抛物线的标准方程为y2=2px(p>0),过M(2,-2$\sqrt{2}$),利用抛物线的定义,求解即可.
(2)直线l斜率为1,且过焦点F(1,0),则l方程:y=x-1,联立方程组,设A(x1,y1),B(x2,y2),利用抛物线的性质,即可线段AB的长度.
解答 解:(1)设抛物线的标准方程为y2=2px(p>0),过M(2,-2$\sqrt{2}$),
得4p=8,即得p=2,
∴抛物线的标准方程为y2=4x
(2)直线l斜率为1,且过焦点F(1,0),则l方程:y=x-1
联立$\left\{\begin{array}{l}y=x-1\\{y}^{2}=4x\end{array}\right.$,
可得x2-6x+1=0,
设A(x1,y1),B(x2,y2),则x1+x2=6
∴|AB|=x1+x2+p=6+2=8即线段AB的长度.
点评 本题考查抛物线的简单性质的应用,抛物线方程的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:
①函数f(x)的极大值点为2;
②函数f(x)在[2,4]上是减函数;
③如果当x∈[m,5]时,f(x)的最小值是-2,那么m的最大值为4;
④函数y=f(x)-a(a∈R)的零点个数可能为0、1、2、3、4个.
其中正确命题的是①②③④.
 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:| x | -1 | 0 | 4 | 5 |
| f(x) | -1 | -2 | -2 | -1 |
②函数f(x)在[2,4]上是减函数;
③如果当x∈[m,5]时,f(x)的最小值是-2,那么m的最大值为4;
④函数y=f(x)-a(a∈R)的零点个数可能为0、1、2、3、4个.
其中正确命题的是①②③④.
20.已知函数f(x)的部分图象如图,则f(x)的解析式可能为( )
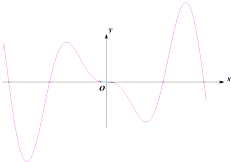

| A. | f(x)=xcosx-sinx | B. | f(x)=xsinx | C. | f(x)=xcosx+sinx | D. | f(x)=xcosx |
 将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),
将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),