题目内容
17．已知等比数列{an}的前n项和为Sn，若$\frac{{S}_{4}}{{a}_{4}}$=$\frac{{S}_{2}}{{a}_{2}}$，则$\frac{{S}_{2015}}{{S}_{1}}$=1．分析 由题意和求和公式可得q的方程，解方程可得q，可得S2015，进而可得比值．
解答 解：由题意可得等比数列{an}的公比q≠1，
∵$\frac{{S}_{4}}{{a}_{4}}$=$\frac{{S}_{2}}{{a}_{2}}$，∴S4a2=S2a4，
∴$\frac{{a}_{1}}{1-q}$（1-q4）•a1q=$\frac{{a}_{1}}{1-q}$（1-q2）•a1q3，
化简并解方程可得q=-1，
∴S2015=$\frac{{a}_{1}}{1-q}$（1-q2015）=a1，
∴$\frac{{S}_{2015}}{{S}_{1}}$=1
故答案为：1．
点评 本题考查等比数列的性质和求和公式，求出数列的公比是解决问题的关键，属基础题
练习册系列答案
全能测控一本好卷系列答案
相关题目
13．
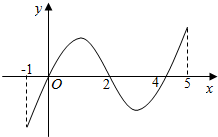已知函数f（x）的定义域为[-1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图所示．下列四个命题：
①函数f（x）的极大值点为2；
②函数f（x）在[2，4]上是减函数；
③如果当x∈[m，5]时，f（x）的最小值是-2，那么m的最大值为4；
④函数y=f（x）-a（a∈R）的零点个数可能为0、1、2、3、4个．
其中正确命题的是①②③④．
已知函数f（x）的定义域为[-1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图所示．下列四个命题：| x | -1 | 0 | 4 | 5 |
| f（x） | -1 | -2 | -2 | -1 |
②函数f（x）在[2，4]上是减函数；
③如果当x∈[m，5]时，f（x）的最小值是-2，那么m的最大值为4；
④函数y=f（x）-a（a∈R）的零点个数可能为0、1、2、3、4个．
其中正确命题的是①②③④．
12．“金能导电，银能导电，铜能导电，铁能导电，所有一切金属都能导电．”此推理方法是（ ）
| A． | 归纳推理 | B． | 类比推理 | C． | 演绎推理 | D． | 以上均有可能 |
2．已知α，β都是锐角，cosα=$\frac{3}{5}$，cos（α+β）=-$\frac{\sqrt{2}}{2}$，则cosβ的值为（ ）
| A． | -$\frac{7\sqrt{2}}{10}$ | B． | $\frac{\sqrt{2}}{10}$ | C． | $\frac{\sqrt{2}}{5}$ | D． | $\frac{7\sqrt{2}}{5}$ |
7．为了解某市民众对政府出台楼市限购令的情况，在该市随机抽取了50名市民进行调查，他们月收人（单位：百元）的频数分布及对楼市限购令赞成的人数如下表：
将月收入不低于55的人称为“高收人族”，月收入低于55的人称为“非高收入族”．
（Ⅰ）根据已知条件完成下面的2x2列联表，问赞成楼市限购令与收入高低是否有关？
（Ⅱ）现从月收入在[15，25）的人中随机抽取两人，所抽取的两人都赞成楼市限购令的概率．
附：${x^2}=\frac{{n{{（{n_{11}}{n_{22}}-{n_{12}}{n_{21}}）}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}，\frac{{p（{x^2}≥k）}}{k}\frac{0.050.01}{3.8416.635}$）
| 月收入 | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75） |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
（Ⅰ）根据已知条件完成下面的2x2列联表，问赞成楼市限购令与收入高低是否有关？
| 非高收入族 | 高收入族 | 总计 | |
| 赞成 | |||
| 不赞成 | |||
| 总计 |
附：${x^2}=\frac{{n{{（{n_{11}}{n_{22}}-{n_{12}}{n_{21}}）}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}，\frac{{p（{x^2}≥k）}}{k}\frac{0.050.01}{3.8416.635}$）