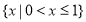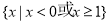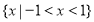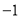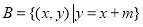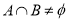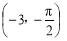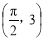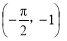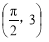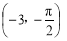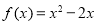题目内容
已知幂函数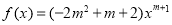 为偶函数.
为偶函数.
(1)求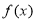 的解析式;
的解析式;
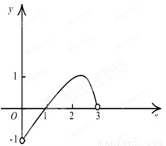
(2)若函数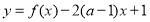 在区间(2,3)上为单调函数,求实数
在区间(2,3)上为单调函数,求实数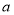 的取值范围.
的取值范围.
(1)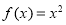 ;(2)
;(2)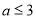 或
或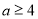
【解析】
试题分析:(1)因为函数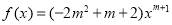 为幂函数,所以
为幂函数,所以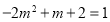 ,所以解得
,所以解得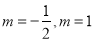 .所以函数
.所以函数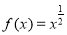 或
或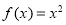 .又因为函数
.又因为函数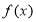 为偶函数,所以函数
为偶函数,所以函数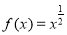 不符合舍去.所以
不符合舍去.所以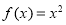 .本小题关键是考查幂函数的概念.
.本小题关键是考查幂函数的概念.
(2)由(1)得函数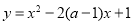 .因为二次函数的对称轴
.因为二次函数的对称轴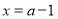 .又因为函数
.又因为函数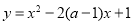 在区间(2,3)上为单调函数.所以函数的对称轴在区间(2,3)外面所以得到两个不等式即可求得
在区间(2,3)上为单调函数.所以函数的对称轴在区间(2,3)外面所以得到两个不等式即可求得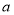 的范围.
的范围.
试题解析:(1)由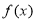 为幂函数知
为幂函数知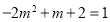 ,得
,得 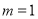 或
或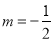 3分
3分
当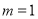 时,
时,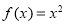 ,符合题意;当
,符合题意;当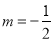 时,
时,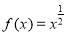 ,不合题意,舍去.
,不合题意,舍去.
∴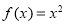 . 6分
. 6分
(2)由(1)得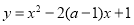 ,
,
即函数的对称轴为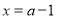 , 8分
, 8分
由题意知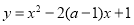 在(2,3)上为单调函数,
在(2,3)上为单调函数,
所以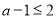 或
或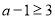 , 11分
, 11分
即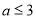 或
或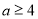 . 12分
. 12分
考点:1.基本初等函数的一般式.2.二次函数的单调性.

练习册系列答案
相关题目