题目内容
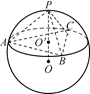
如图,在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积.

3πa2
如题图,设过A、B、C三点的球的截面圆半径为r,圆心为O′,球心到该圆面的距离为d,在三棱锥PABC中,
∵PA、PB、PC两两垂直,PA=PB=PC=a,∴AB=AC=BC=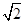 a,
a,
且点P在△ABC内的射影是△ABC的中心O′,由正弦定理,得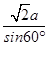 =2r,∴r=
=2r,∴r=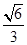 a.
a.
又根据球的截面圆性质,有OO′⊥平面ABC,而PO′⊥平面ABC,
∴P、O、O′三点共线,球的半径R=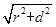 .又PO′=
.又PO′=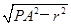 =
=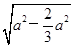 =
=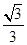 a,
a,
∴OO′=R-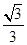 a=d=
a=d=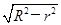 ,∴
,∴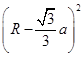 =R2-
=R2-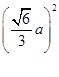 ,解得R=
,解得R=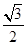 a.
a.
∴S球=4πR2=3πa2.
∵PA、PB、PC两两垂直,PA=PB=PC=a,∴AB=AC=BC=
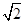 a,
a,且点P在△ABC内的射影是△ABC的中心O′,由正弦定理,得
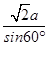 =2r,∴r=
=2r,∴r=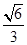 a.
a.又根据球的截面圆性质,有OO′⊥平面ABC,而PO′⊥平面ABC,
∴P、O、O′三点共线,球的半径R=
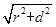 .又PO′=
.又PO′=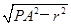 =
=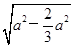 =
=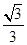 a,
a,∴OO′=R-
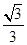 a=d=
a=d=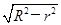 ,∴
,∴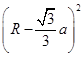 =R2-
=R2-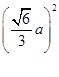 ,解得R=
,解得R=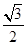 a.
a.∴S球=4πR2=3πa2.

练习册系列答案
相关题目
 的边长为3,
的边长为3, 与
与 交于
交于 ,且
,且 .将菱形
.将菱形 折起得到三棱锥
折起得到三棱锥 (如图),点
(如图),点 是棱
是棱 的中点,
的中点, .
.
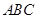
 平面
平面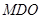 ;
; 的体积.
的体积.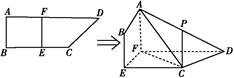
 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
 倍,那么该圆锥的侧面展开图扇形的圆心角为( )
倍,那么该圆锥的侧面展开图扇形的圆心角为( )




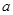 ,点
,点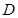 是
是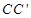 上任意一点,连接
上任意一点,连接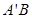 ,
,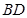 ,
,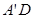 ,
,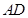 ,则三棱锥
,则三棱锥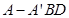 的体积为( )
的体积为( )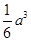
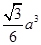

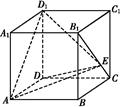
 A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A
A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A