题目内容
【题目】已知函数,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 有
有![]() 个不同的零点,求实数
个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时
时![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() 在
在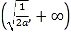 上单调递增,
上单调递增,![]() 在
在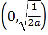 上单调递减.(2)
上单调递减.(2)![]()
【解析】
(1)分![]() 两种情况讨论导数的符号后可得函数的单调区间.
两种情况讨论导数的符号后可得函数的单调区间.
(2)根据(1)可知![]() 且
且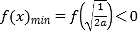 ,后者可得实数
,后者可得实数![]() 的取值范围为
的取值范围为![]() ,再根据
,再根据![]() ,
,![]() 结合零点存在定理可知当
结合零点存在定理可知当![]() 时函数确有两个不同的零点.
时函数确有两个不同的零点.
(1)解:因为![]() ,
,
①当![]() 时,总有
时,总有![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
②当![]() 时,令
时,令![]() ,解得
,解得![]() .
.
故![]() 时,
时,![]() ,所以
,所以![]() 在
在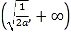 上单调递增.
上单调递增.
同理![]() 时,有
时,有![]() ,所以
,所以![]() 在
在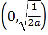 上单调递减.
上单调递减.
(2)由(1)知当![]() 时,
时,![]() 单调递减,
单调递减,
所以函数![]() 至多有一个零点,不符合已知条件,
至多有一个零点,不符合已知条件,
由(1)知当![]() 时,
时,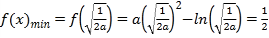
![]() ,
,
所以![]() 当时,解得
当时,解得![]() ,从而
,从而![]() .
.
又![]() 时,有
时,有![]() ,因为
,因为![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 为增函数,故
为增函数,故![]() ,
,
所以![]() ,根据零点存在定理可知:
,根据零点存在定理可知:
![]() 在
在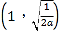 内有一个零点,在
内有一个零点,在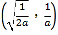 内有一个零点,
内有一个零点,
故当函数![]() 有
有![]() 个零点时,
个零点时,![]() 的取值范围为
的取值范围为![]() .
.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,下表是在某单位调查后得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:
①从赞同“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行陈述发言,求事件“男士和女士各至少有
人进行陈述发言,求事件“男士和女士各至少有![]() 人发言”的概率;
人发言”的概率;
②从反对“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行座谈,设选出的
人进行座谈,设选出的![]() 人中女士人数为
人中女士人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
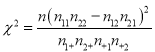
【题目】某公司为了鼓励运动提高所有用户的身体素质,特推出一款运动计步数的软件,所有用户都可以通过每天累计的步数瓜分红包,大大增加了用户走步的积极性,所以该软件深受广大用户的欢迎.该公司为了研究“日平均走步数和性别是否有关”,统计了2019年1月份所有用户的日平均步数,规定日平均步数不少于8000的为“运动达人”,步数在8000以下的为“非运动达人”,采用按性别分层抽样的方式抽取了100个用户,得到如下列联表:
运动达人 | 非运动达人 | 总计 | |
男 | 35 | 60 | |
女 | 26 | ||
总计 | 100 |
(1)(i)将![]() 列联表补充完整;
列联表补充完整;
(ii)据此列联表判断,能否有![]() 的把握认为“日平均走步数和性别是否有关”?
的把握认为“日平均走步数和性别是否有关”?
(2)从样本中的运动达人中抽取7人参加“幸运抽奖”活动,通过抽奖共产生2位幸运用户,求这2位幸运用户恰好男用户和女用户各一位的概率.
附:
|
|
|
|
|
|
|
|