题目内容
【题目】已知圆![]() 和
和![]() 轴相切,并且圆心
轴相切,并且圆心![]() 在直线
在直线![]() 上.
上.
(1)如果圆![]() 和
和![]() 轴相切于点
轴相切于点![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)如果圆![]() 被直线
被直线![]() 截得的弦长为
截得的弦长为![]() ,求圆
,求圆![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】
(1)根据圆![]() 和
和![]() 轴相切于点
轴相切于点![]() 和圆心
和圆心![]() 在直线
在直线![]() 上,可以求出圆心的坐标,再根据切线的性质可以求出圆的半径,最后求出圆的方程;
上,可以求出圆心的坐标,再根据切线的性质可以求出圆的半径,最后求出圆的方程;
(2)设出圆心的坐标,根据切线性质可以求出关径,再根据点到直线的距离公式、垂径定理以及勾股定理,可以求出圆心的坐标和半径的大小,最后写出圆的方程即可.
解:(1)圆心C在直线y=1上,圆心在直线x-3y=0上,
所以圆心C的坐标为(3,1),由圆C和y轴相切,得半径为3,
所以所求圆C的方程为![]() ;
;
(2)设圆心为(3t,t),半径为r=|3t|,
则圆心到直线y=x的距离![]() ,
,
而![]() ,即
,即![]() ,解得t=±1,
,解得t=±1,
∴![]() 或
或![]() .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】为了解某班学生喜欢打篮球是否与性别有关,对本班50人进行了问卷调查,得到如表的![]() 列联表:
列联表:
喜欢打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中喜欢打篮球的学生为30人.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜欢打篮球与性别有关?请说明你的理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
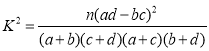 ,其中
,其中![]() .
.
【题目】某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
|
|
|
|
|
|
企业数 | 2 | 24 | 53 | 14 | 7 |
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
附:![]() .
.