题目内容
已知f(x)=x2+ax+b,g(x)=x2+cx+d,又f(2x+1)=4g(x),且f′(x)=g′(x),f(5)=30,则g(4)= ( )
A.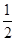 |
B.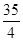 |
C.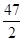 |
D.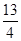 |
C
题设中有四个参数a、b、c、d,为确定它们的值需要四个方程.
由f(2x+1)=4g(x),得4x2+2(a+2)x+(a+b+1)=4x2+4cx+4d.
于是有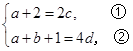
由f′(x)=g′(x),得2x+a=2x+c,∴a=c.③
由f(5)=30,得25+5a+b=30.④
∴由①③可得a=c=2.
由④得b=-5,再由②得d=-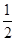
∴g(x)=x2+2x-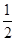 .故g(4)=16+8-
.故g(4)=16+8-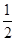 =
=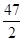 .
.
由f(2x+1)=4g(x),得4x2+2(a+2)x+(a+b+1)=4x2+4cx+4d.
于是有
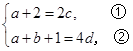
由f′(x)=g′(x),得2x+a=2x+c,∴a=c.③
由f(5)=30,得25+5a+b=30.④
∴由①③可得a=c=2.
由④得b=-5,再由②得d=-
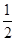
∴g(x)=x2+2x-
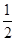 .故g(4)=16+8-
.故g(4)=16+8-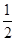 =
=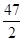 .
.
练习册系列答案
相关题目
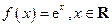 .
.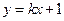 与
与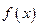 的反函数的图象相切,求实数k的值;
的反函数的图象相切,求实数k的值; ,讨论曲线
,讨论曲线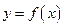 与曲线
与曲线 公共点的个数;
公共点的个数;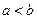 ,比较
,比较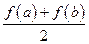 与
与 的大小,并说明理由.
的大小,并说明理由.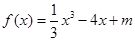 在区间
在区间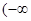 ,
,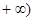 上有极大值
上有极大值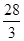 .
.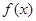 在区间
在区间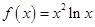 .
.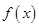 的单调区间;
的单调区间;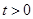 ,存在唯一的
,存在唯一的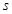 ,使
,使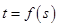 ;
;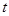 的函数为
的函数为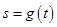 ,证明:当
,证明:当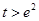 时,有
时,有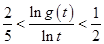 .
.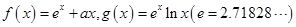 ..
..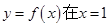 处的切线为
处的切线为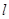 ,点(1,0)到直线l的距离为
,点(1,0)到直线l的距离为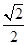 ,求a的值;
,求a的值;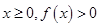 恒成立,试确定
恒成立,试确定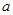 的取值范围;
的取值范围;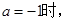 是否存在实数
是否存在实数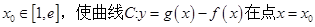 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出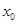 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 的大小关系 ( )
的大小关系 ( )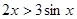
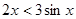
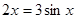
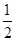 πr2
πr2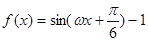
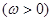 的导数
的导数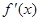 的最大值为3,则
的最大值为3,则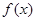 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是 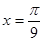
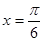
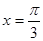
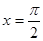
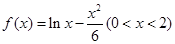 ,则( )
,则( )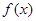 有最小值
有最小值