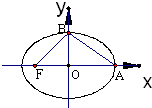
题目内容

椭圆
x2
4
+y2=1的左、右焦点分别为F1，F2，点P在椭圆上，若P，F1，F2是一个直角三角形的三个顶点，则点P到x轴的距离为（　　）
A．
1
2
B．
3
3
C．
1
2
或
3
3
D．以上均不对
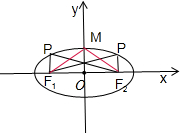
如图所示，
∵椭圆
x2
4
+y2=1，∴a2=4，b2=1，c=
a2-b2
=
3
．
设点M是椭圆的短轴的上顶点，则∠F1MF2是椭圆上的点与点F1，F2张开的最大角，而tan∠F2OM=
3
，∴∠F2OM=60°，
∴∠F1OF2=120°，∴点P不可能是直角顶点．
当PF2⊥x轴或PF1⊥x轴时，把x=c=
3
代入椭圆的方程可得：
(
3
)2
4
+y2=1，解得y=±
1
2
．
∴|PF1|=|PF2|=
1
2
．
∴点P到x轴的距离是
1
2
．
故选：A．
练习册系列答案
相关题目
已知点P为椭圆
x2
45
+
y2
20
=1上且位于在第三象限内一点，且它与两焦点连线互相垂直，若点P到直线4x-3y-2m+1=0的距离不大于3，则实数m的取值范围是______．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，其左、右两焦点分别为F1、F2．直线L经过椭圆C的右焦点F2，且与椭圆交于A、B两点．若A、B、F1构成周长为4
2
的△ABF1，椭圆上的点离焦点F2最远距离为
2
+1，且弦AB的长为
4
2
3
，求椭圆和直线L的方程．
如图，椭圆中心在坐标原点，F为左焦点，当
FB
⊥
AB
时，其离心率为
5
-1
2
，此类椭圆被称为“黄金椭圆”，类比“黄金椭圆”，可推算出“黄金双曲线”的离心率为（　　）
A．
5
+1
2
B．
5
-1
2
C．
5
+1		D．
5
-1
已知动点P（x，y）满足：
(x+1)2+y2
+
(x-1)2+y2
=4，则点P的轨迹的离心率是______．
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上任意一点到两焦点的距离分别为d1，d2，焦距为2c，若d1，2c，d2成等差数列，则椭圆的离心率为（　　）
A．
1
2
B．
2
2
C．
3
2
D．
3
4
椭圆：
x2
a2
+
y2
b2
=1（a＞b＞0），左右焦点分别是F1，F2，焦距为2c，若直线y=
3
(x+c)与椭圆交于M点，满足∠MF1F2=2∠MF2F1，则离心率是（　　）
A．
2
2
B．
3
-1		C．
3
-1
2
D．
3
2
动点P为椭圆
x2
25
+
y2
16
=1上任意一点，左右焦点分别是F1，F2，直线l为∠F1PF2的外角平分线，过F1作直线l的垂线，垂足为Q，则点Q的轨迹方程是（　　）
A．x2+y2=25B．x2+y2=16C．x2-y2=25D．x22y2=16
椭圆2x2+3y2=6的焦距是（　　）
A．2(
3
-
2
)		B．2C．2
5
D．2(
3
+
2
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网