题目内容
已知正项等比数列
满足：
,若存在两项
使得
，则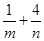
的最小值为( )
| A．9 | B． | C． | D． |
D
解析试题分析：利用等比数列的知识求出m与n的关系，在利用基本不等式求解出最值.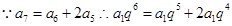
即
.又因为
所以
.故答案为D
考点：等比数列、基本不等式
练习册系列答案
相关题目
在等差数列{an}中，其前n项和是
，若
，则在
中最大的是( )
A． | B． | C． | D． |
已知数列{
}中，
=
，
+
（n
，则数列{}的通项公式为（ ）
A． | B． |
C． | D． |
已知数列{an}的通项公式
,则
=( )
| A．2012 | B．2013 | C．2014 | D．2015 |
若数列{an}的通项公式是
，则该数列的第五项为（ ）
| A．1 | B．-1 | C． | D．- |
已知函数
的图象与直线
交于点P，若图象在点P处的切线与x轴交点的横坐标为
，则
＋
＋…＋
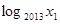的值为（ ）
| A．－1 | B．1－log20132012 | C．-log20132012 | D．1 |
在函数y＝f(x)的图象上有点列(xn，yn)，若数列{xn}是等差数列，数列{yn}是等比数列，则函数y＝f(x)的解析式可能为( )
| A．f(x)＝2x＋1 | B．f(x)＝4x2 |
| C．f(x)＝log3x | D．f(x)＝ x |
1202年，意大利数学家斐波那契在他的书中给出了一个关于兔子繁殖的递推关系：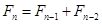
（
），其中
表示第
个月的兔子的总对数，
，则
的值为（ ）
| A．13 | B．21 | C．34 | D．55 |
已知正项数列{an}满足a1＝1，(n＋2)an＋12－(n＋1)
＋anan＋1＝0，则它的通项公式为( )．
A．an＝ | B．an＝ |
C．an＝ | D．an＝n |