题目内容
20．在正方体ABCD-A1B1C1D1中，AB=2，点A，B，C，D在球O上，球O与BA1的另一个交点为E，且AE⊥BA1，则球O的表面积为 （ ）| A． | 6π | B． | 8π | C． | 12π | D． | 16π |
分析 设与CD1的另一个交点为F，连结EF，DF，得BCEF是矩形，则三棱柱ABE-DCF是球O的内接直三棱柱，求出球O的半径，即可求出球O表面积．
解答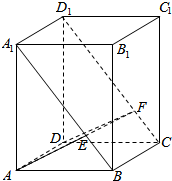 
解：设与CD1的另一个交点为F，连结EF，DF，得BCEF是矩形，
则三棱柱ABE-DCF是球O的内接直三棱柱，
∵正方体ABCD-A1B1C1D1中，AB=2，AE⊥BA1，
∴AE=BE=$\sqrt{2}$，
∴球O的半径R=$\sqrt{2}$，
∴球O表面积为：4πR2=4π•（$\sqrt{2}$）2=8π．
故选：B．
点评 本题主要考查球的表面积公式，以及球内接三棱柱的关系，考查空间想象能力以及计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．等差数列{an}的前n项和为Sn，若a1008=$\frac{1}{2}$，则S2015的值是（ ）
| A． | $\frac{2015}{2}$ | B． | $\frac{2017}{2}$ | C． | 2015 | D． | 2016 |
5．集合A={（x，y）|y=$\frac{{x}^{2}-4}{x+2}$}，B={（x，y）|y=x-2}，则集合A、B的关系是（ ）
| A． | B⊆A | B． | A?B | C． | A=B | D． | 以上均不对 |