题目内容
已知函数f(x)对于一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,则当x∈(0,
),不等式f(x)+2<logax恒成立时,实数a的取值范围是______.
| 1 |
| 2 |
∵f(x)对于一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,
∴令y=0,x=1代入已知式子f(x+y)-f(y)=(x+2y+1)x,
得f(1)-f(0)=2,
∵f(1)=0,
∴f(0)=-2;
令y=0得f(x)+2=(x+1)x,
∴f(x)=x2+x-2.
当x∈(0,
),不等式f(x)+2<logax恒成立时,
即x2+x<logax恒成立,
设g(x)=x2+x,在(0,
)上是增函数,
∴0<g(x)<
,
∴要使x2+x<logax恒成立,
则logax≥
在x∈(0,
)恒成立,
若a>1时,不成立.
若0<a<1,则有loga
=
时,a=
,
∴要使logax≥
在x∈(0,
)恒成立,
则
≤a<1,
故答案为:[
,1)
∴令y=0,x=1代入已知式子f(x+y)-f(y)=(x+2y+1)x,
得f(1)-f(0)=2,
∵f(1)=0,
∴f(0)=-2;
令y=0得f(x)+2=(x+1)x,
∴f(x)=x2+x-2.
当x∈(0,
| 1 |
| 2 |
即x2+x<logax恒成立,
设g(x)=x2+x,在(0,
| 1 |
| 2 |
∴0<g(x)<
| 3 |
| 4 |
∴要使x2+x<logax恒成立,
则logax≥
| 3 |
| 4 |
| 1 |
| 2 |
若a>1时,不成立.
若0<a<1,则有loga
| 1 |
| 2 |
| 3 |
| 4 |
| |||
| 4 |
∴要使logax≥
| 3 |
| 4 |
| 1 |
| 2 |
则
| |||
| 4 |
故答案为:[
| |||
| 4 |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
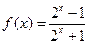 ,(Ⅰ)证明函数
,(Ⅰ)证明函数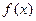 是R上的增函数;
是R上的增函数;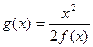 .判定函数
.判定函数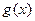 的奇偶性,并证明
的奇偶性,并证明