题目内容
设f(x)是定义在R上的奇函数,且f(x+3)f(x)=-1,f(-2)=1,则f(2012)=______.
∵f(x+3)f(x)=-1,
∴用x+3代替x,得f(x+6)f(x+3)=-1,
由此可得f(x+6)=f(x),得函数的最小正周期T=6
∴f(2012)=f(335×6+2)=f(2)
∵f(x)是定义在R上的奇函数,且f(-2)=1
∴f(2)=-f(-2)=-1
故答案为:-1
∴用x+3代替x,得f(x+6)f(x+3)=-1,
由此可得f(x+6)=f(x),得函数的最小正周期T=6
∴f(2012)=f(335×6+2)=f(2)
∵f(x)是定义在R上的奇函数,且f(-2)=1
∴f(2)=-f(-2)=-1
故答案为:-1

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
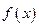 =
=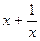 .(1)判断
.(1)判断 上的单调性并加以证明.
上的单调性并加以证明.