题目内容
二次函数f(x)=x2+2ax+2a+1.
(1)若对任意x∈R有f(x)≥1恒成立,求实数a的取值范围;
(2)讨论函数f(x)在区间[0,1]上的单调性;
(3)若对任意的x1,x2∈[0,1]有|f(x1)-f(x2)|≤1恒成立,求实数a的取值范围.
(1)若对任意x∈R有f(x)≥1恒成立,求实数a的取值范围;
(2)讨论函数f(x)在区间[0,1]上的单调性;
(3)若对任意的x1,x2∈[0,1]有|f(x1)-f(x2)|≤1恒成立,求实数a的取值范围.
(1)f(x)≥1?x2+2ax+2a≥0对任意x∈R恒成立,
∴△=4a2-8a≤0,解得0≤a≤2,
∴a的范围是[0,2];
(2)f(x)=(x+a)2-a2+2a+1,其图象是开口向上的抛物线,对称轴方程为x=-a,
讨论:①当-a≤0即a≥0时,f(x)在区间[0,1]上单调递增;
②当0<-a<1即-1<a<0时,f(x)在区间[0,-a]上单调递减,在区间[-a,1]上单调递增;
③当-a≥1即a≤-1时,f(x)在区间[0,1]上单调递减.
(3)由题意知,|f(x1)-f(x2)|≤1恒成立等价于f(x)max-f(x)min≤1,
f(0)=2a+1,f(1)=4a+2,f(-a)=-a2+2a+1,
由(2),
或
或
,
解得-1≤a≤0.
∴△=4a2-8a≤0,解得0≤a≤2,
∴a的范围是[0,2];
(2)f(x)=(x+a)2-a2+2a+1,其图象是开口向上的抛物线,对称轴方程为x=-a,
讨论:①当-a≤0即a≥0时,f(x)在区间[0,1]上单调递增;
②当0<-a<1即-1<a<0时,f(x)在区间[0,-a]上单调递减,在区间[-a,1]上单调递增;
③当-a≥1即a≤-1时,f(x)在区间[0,1]上单调递减.
(3)由题意知,|f(x1)-f(x2)|≤1恒成立等价于f(x)max-f(x)min≤1,
f(0)=2a+1,f(1)=4a+2,f(-a)=-a2+2a+1,
由(2),
|
|
|
解得-1≤a≤0.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
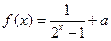 是奇函数,则
是奇函数,则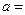 .
. 
