题目内容
9.已知数列{an}的前n项和为Sn,且a1=$\frac{1}{2}$,an=-2SnSn-1(n≥2),则S100=$\frac{1}{200}$.分析 an=-2SnSn-1(n≥2),变形为$\frac{1}{{S}_{n}}-\frac{1}{{S}_{n-1}}$=2,利用等差数列的通项公式即可得出.
解答 解:∵an=-2SnSn-1(n≥2),
∴Sn-Sn-1=-2SnSn-1,
化为$\frac{1}{{S}_{n}}-\frac{1}{{S}_{n-1}}$=2,
∴数列$\{\frac{1}{{S}_{n}}\}$为等差数列,首项为2,公差为2,
∴$\frac{1}{{S}_{n}}$=2+2(n-1)=2n,
∴Sn=$\frac{1}{2n}$.
∴S100=$\frac{1}{200}$.
故答案为:$\frac{1}{200}$.
点评 本题考查了递推式的应用、等差数列的通项公式,考查了变形能力、推理能力与计算能力,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
12.设集合A={x|1<x<4},集合B={x|-1≤x≤3},则A∩(∁RB)等于( )
| A. | (1,4) | B. | (3,4) | C. | (1,3) | D. | (1,2)∪(3,4) |
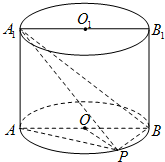 如图,ABB1A1为圆柱的轴截面,点P为圆柱下底面圆周上异于A,B的一点.求证:BP⊥A1P.
如图,ABB1A1为圆柱的轴截面,点P为圆柱下底面圆周上异于A,B的一点.求证:BP⊥A1P.