题目内容
【题目】如图,在四边形ABCD中,AB=BC=2,∠ABC=90°,DA=DC= ![]() .现沿对角线AC折起,使得平面DAC⊥平面ABC,此时点A,B,C,D在同一个球面上,则该球的体积是( )
.现沿对角线AC折起,使得平面DAC⊥平面ABC,此时点A,B,C,D在同一个球面上,则该球的体积是( ) 
A.![]()
B.![]()
C.![]()
D.12π
【答案】A
【解析】解:在图2中,取AC的中点E,连结DE,BE, ∵AD=CD,∴DE⊥AC,
∵平面ACD∩平面ABC=AC,平面ACD⊥平面ABC,
DE平面ACD,
∴DE⊥平面ABC,
∵∠ABC=90°,
∴棱锥外接球的球心O在直线DE上,
∵AD=CD= ![]() ,AB=BC=2,∠ABC=90°,
,AB=BC=2,∠ABC=90°,
∴BE=AE=CE= ![]() AC=
AC= ![]() ,DE=
,DE= ![]() =2,
=2,
设OE=x,则OD=2﹣x,OB= ![]() =
= ![]() ,
,
∴2﹣x= ![]() ,解得x=
,解得x= ![]() ,
,
∴外接球的半径r=2﹣x= ![]() ,
,
∴外接球的体积V= ![]() =
= ![]() ×(
×( ![]() )3=
)3= ![]() .
.
故选A.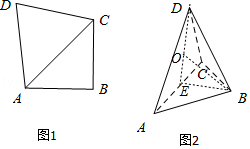
【考点精析】解答此题的关键在于理解球内接多面体的相关知识,掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长.

练习册系列答案
相关题目
