题目内容

【题目】70年代中期，美国各所名牌大学校园内，人们都像发疯一般，夜以继日，废寝忘食地玩一个数学游戏．这个游戏十分简单：任意写出一个自然数N，并且按照以下的规律进行变换：如果是个奇数，则下一步变成3N+1；如果是个偶数，则下一步变成 ．不单单是学生，甚至连教师、研究员、教授与学究都纷纷加入．为什么这个游戏的魅力经久不衰？因为人们发现，无论N是怎样一个数字，最终都无法逃脱回到谷底1．准确地说，是无法逃出落入底部的4﹣2﹣1循环，永远也逃不出这样的宿命．这就是著名的“冰雹猜想”．按照这种运算，自然数27经过十步运算得到的数为（ ）
A.142
B.71
C.214
D.107

【答案】C
【解析】解：27→82→41→124→62→31→94→47→142→71→214， 故选：C
【考点精析】解答此题的关键在于理解归纳推理的相关知识，掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理．

练习册系列答案
相关题目

【题目】已知 ，函数 .
（1）当 时，解不等式 ；
（2）若关于 的方程 的解集中恰好有一个元素，求 的取值范围；
（3）设 ，若对任意 ，函数 在区间 上的最大值与最小值的差不超过1，求 的取值范围.

【题目】已知，函数.

（1）当时，解不等式；

（2）若关于的方程的解集中恰好有一个元素，求的取值范围；

（3）设，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.

【题目】已知函数 ，a∈R．
（Ⅰ）当a∈[1，e2]时，讨论函数f（x）的零点的个数；
（Ⅱ）令g（x）=tx2﹣4x+1，t∈[﹣2，2]，当a∈[1，e]时，证明：对任意的 ，存在x2∈[0，1]，使得f（x1）=g（x2）．

【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了至月份每月号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：

日期

1月10日

2月10日

3月10日

4月10日

5月10日

6月10日

昼夜温差

（）

就诊人数（个）

该兴趣小组确定的研究方案是：先从这六组数据中选取组，用剩下的组数据求线性回归方程，再用被选取的组数据进行检验.

（1）求选取的组数据恰好是相邻两月的概率；

（2）若选取的是1月与月的两组数据，请根据2至5月份的数据，求出关于的线性回归方程；

（3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想？

参考数据，

（参考公式： ，）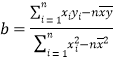

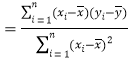【题目】如图，在四边形ABCD中，AB=BC=2，∠ABC=90°，DA=DC= ．现沿对角线AC折起，使得平面DAC⊥平面ABC，此时点A，B，C，D在同一个球面上，则该球的体积是（ ）
A.
B.
C.
D.12π

【题目】过点P（2，0）的直线交抛物线y2=4x于A，B两点，若抛物线的焦点为F，则△ABF面积的最小值为 ．

【题目】已知圆 的有 条弦，且任意两条弦都彼此相交，任意三条弦不共点，这 条弦将圆 分成了 个区域，（例如：如图所示，圆 的一条弦将圆 分成了2（即 ）个区域，圆 的两条弦将圆 分成了4（即 ）个区域，圆 的3条弦将圆 分成了7（即 ）个区域），以此类推，那么 与 之间的递推式关系为： ．

【题目】已知椭圆 的一个顶点为A(2，0)，离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M、N.
（1）求椭圆C的方程.
（2）当△AMN的面积为 时，求k的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网