题目内容
12.已知0<k<4,直线l1:kx-2y-2k+8=0和直线${l_2}:2x+{k^2}y-4{k^2}-4=0$与两坐标轴围成一个四边形,求使这个四边形面积取最小时的k的值及最小面积的值.分析 求出两直线经过的定点坐标,再求出直线与x 轴的交点,与y 轴的交点,得到所求的四边形,求出四边形的面积表达式,应用二次函数的知识求面积最小时的k值与最小面积值.
解答 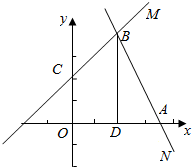 解:如图所示:
解:如图所示:
直线L:kx-2y-2k+8=0 即k(x-2)-2y+8=0,过定点B(2,4),
与y轴的交点C(0,4-k),
直线M:2x+k2y-4k2-4=0,即 2x+k2 (y-4)-4=0,
过定点(2,4 ),与x轴的交点A(2k2+2,0),
由题意,四边形的面积等于三角形ABD的面积和梯形 OCBD的面积之和,
∴所求四边形的面积为$\frac{1}{2}$×4×(2 k2+2-2)+$\frac{1}{2}$×(4-k+4)×2=4k2-k+8,
∴当k=$\frac{1}{8}$时,所求四边形的面积最小,最小面积的值为$\frac{63}{8}$.
点评 本题考查了直线过定点问题,以及二次函数的最值问题,考查了数形结合思想的应用问题,是基础题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
 如图所示,已知空间四边形OABC各边及对角线长都相等,E,F分别为AB,OC的中点,求0E与BF所成角的余弦值.
如图所示,已知空间四边形OABC各边及对角线长都相等,E,F分别为AB,OC的中点,求0E与BF所成角的余弦值.