题目内容
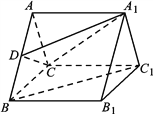
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2) ![]()
【解析】试题分析:(Ⅰ)首先利用正弦定理求得![]() ,由此可推出
,由此可推出![]() ,然后利用勾股定理推出
,然后利用勾股定理推出![]() ,从而使问题得证;(Ⅱ)以点
,从而使问题得证;(Ⅱ)以点![]() 为坐标原点建立空间直角坐标系,然后求出相关点的坐标与向量,从而求得平面
为坐标原点建立空间直角坐标系,然后求出相关点的坐标与向量,从而求得平面![]() 与平面
与平面![]() 的法向量,进而利用空间夹角公式求解.
的法向量,进而利用空间夹角公式求解.
试题解析:(Ⅰ)证明:在![]() 中,
中, ![]() ,由已知
,由已知![]() ,
, ![]() ,
, ![]() ,
,
解得![]() ,所以
,所以![]() ,即
,即![]() ,可求得
,可求得![]() .
.
在![]() 中,
中,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)过![]() 作直线
作直线![]() 垂直于
垂直于![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
∵由(Ⅰ)可知,平面![]() 平面
平面![]() ,∴
,∴![]() 在平面
在平面![]() 上的投影一定在
上的投影一定在![]() 上,过
上,过![]() 作
作![]() 于
于![]() ,则
,则![]() ,
, ![]() ,则
,则![]() ,
,
易求![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
, 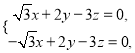 解得
解得![]() .
.
同理可求得平面![]() 的法向量
的法向量![]() ,
,
∴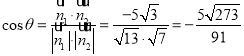 .
.


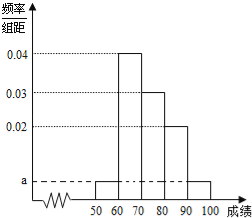
【题目】某中学为了了解全校学生的阅读情况,在全校采用随机抽样的方法抽取了60名学生(其中初中组和高中组各30名)进行问卷调查,并将他们在一个月内去图书馆的次数进行了统计,将每组学生去图书馆的次数分为5组: ![]() ,分别制作了如图所示的频率分布表和频率分布直方图.
,分别制作了如图所示的频率分布表和频率分布直方图.
分组 | 人数 | 频率 |
| 3 | |
| 9 | |
| 9 | |
| 0.2 | |
| 0.1 |
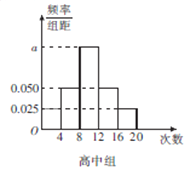
(1)完成频率分布表,并求出频率分布直方图中![]() 的值;
的值;
(2)在抽取的60名学生中,从在一个月内去图书馆的次数不少于16次的学生中随机抽取3人,并用![]() 表示抽得的高中组的人数,求
表示抽得的高中组的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】2017年5月13日第30届大连国际马拉松赛举行,某单位的10名跑友报名参加了半程马拉松、10公里健身跑、迷你马拉松3个项目(每人只报一项),报名情况如下:
项目 | 半程马拉松 | 10公里健身跑 | 迷你马拉松 |
人数 | 2 | 3 | 5 |
(其中:半程马拉松![]() 公里,迷你马拉松
公里,迷你马拉松![]() 公里)
公里)
(1)从10人中选出2人,求选出的两人赛程距离之差大于10公里的概率;
(2)从10人中选出2人,设![]() 为选出的两人赛程距离之和,求随机变量
为选出的两人赛程距离之和,求随机变量![]() 的分布列.
的分布列.