题目内容
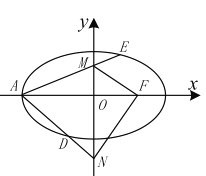
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
, ![]() 为原点,
为原点, ![]() ,
, ![]() 是
是![]() 轴上的两个动点,且
轴上的两个动点,且![]() ,直线
,直线![]() 和
和![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
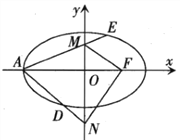
(Ⅰ)求![]() 的面积的最小值;
的面积的最小值;
(Ⅱ)证明: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
【答案】(1)1;(2)详见解析。
【解析】试题分析:(Ⅰ)设![]() ,
, ![]() ,然后根据
,然后根据![]() 求得
求得![]() 的值,从而得到
的值,从而得到![]() 的表达式,从而利用基本不等式求出最小值,;(Ⅱ)首先设出直线
的表达式,从而利用基本不等式求出最小值,;(Ⅱ)首先设出直线![]() 的方程,然后联立椭圆方程,利用韦达定理得到点
的方程,然后联立椭圆方程,利用韦达定理得到点![]() 坐标间的关系,从而使问题得证.
坐标间的关系,从而使问题得证.
试题解析:(Ⅰ)设![]() ,
, ![]() ,∵
,∵![]() ,可得
,可得![]() ,
,
![]() ,
,
∵![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 的面积的最小值为1.
的面积的最小值为1.
(Ⅱ)∵![]() ,
, ![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,
,
由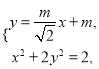 得
得![]() ,
,
由![]() ,得
,得![]() ,①
,①
同理可得![]() ,
,
∵![]() ,∵
,∵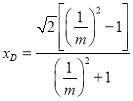
![]() ②
②
故由①②可知: ![]() ,
,
代入椭圆方程可得![]()
∵![]() ,故
,故![]() ,
, ![]() 分别在
分别在![]() 轴两侧,
轴两侧, ![]() ,
,
∴![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
点睛:解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法.

【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用![]() 、
、![]() 、
、![]() 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| 甲 | 4次 | 6次 | 2次 | 12次 |
| 乙 | 3次 | 6次 | 3次 | 12次 |
| 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑到旱情和水土流失,如果甲地恰需中雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只能是小雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【题目】第十二届全国人名代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(1)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
(2)根据题意建立![]() 列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?
列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?
附:  ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】王明参加某卫视的闯关活动,该活动共3关.设他通过第一关的概率为0.8,通过第二、第三关的概率分别为p,q,其中![]() ,并且是否通过不同关卡相互独立.记ξ为他通过的关卡数,其分布列为:
,并且是否通过不同关卡相互独立.记ξ为他通过的关卡数,其分布列为:
ξ | 0 | 1 | 2 | 3 |
P | 0.048 | a | b | 0.192 |
(Ⅰ)求王明至少通过1个关卡的概率;
(Ⅱ)求p,q的值.