Question

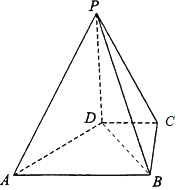
【题目】如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，PD=2，DC=BC=1，AB=2，AB∥DC，∠BCD=90°.

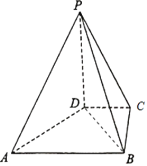
（1）求证：AD⊥PB；

（2）求A点到平面BPC的距离.

Answer 1

【答案】（1）证明见解析.（2）

【解析】

（1）利用勾股定理证得AD⊥BD，又PD⊥平面ABCD，所以PD⊥AD，从而由线面垂直的判定定理得到AD⊥平面PBD，所以AD⊥PB；

（2）证得BC⊥PC，求出S△BPC和S△ABC，再由VA﹣BPC=VP﹣ABC 利用等体积法即可求出点A到平面PBC的距离.

（1）如图所示：

在四边形ABCD中，连接BD，由DC=BC=1，AB=2，∠BCD=∠ABC，

在△ABD中，BD=AD，又AB=2，

因此AD⊥BD，又PD⊥平面ABCD，

∴PD⊥AD，又BD∩PD=D，

∴AD⊥平面PBD，

∴AD⊥PB；

（2）在四棱锥P﹣ABCD中，∵PD⊥平面ABCD，

∴PD⊥BC，而BC⊥DC，

∴BC⊥平面PDC，

∴BC⊥PC，又，

∴，而S△ABC1，

，设点A到平面PBC的距离为h，

由VA﹣BPC=VP﹣ABC 可得：，

∴，

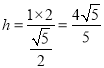即点A到平面PBC的距离为.