题目内容
20.对于函数y=f(x),若其定义域内存在两个实数m,n(m<n),使得x∈[m,n]时,f(x)的值域也是[m,n],则称函数f(x)为“和谐函数”,若函数f(x)=k+$\sqrt{x+2}$是“和谐函数”,则实数k的取值范围是-$\frac{9}{4}$<k≤-2.分析 求出f(x)的定义域,根据f(x)为“和谐函数”,确定出k的范围即可.
解答 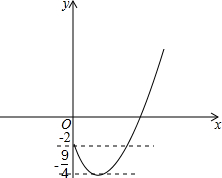 解:根据题意得:函数f(x)=k+$\sqrt{x+2}$是单调增函数,
解:根据题意得:函数f(x)=k+$\sqrt{x+2}$是单调增函数,
∵“和谐函数”的定义为:存在实数m,n,x∈[m,n]时,f(x)∈[m,n],
∴$\left\{\begin{array}{l}{k+\sqrt{m+2}=m}\\{k+\sqrt{n+2}=n}\end{array}\right.$,
∴方程k+$\sqrt{x+2}$=x有两个不等实根.并且得到k=x-$\sqrt{x+2}$,即对于同一个k有两个x对应,
设y=x-$\sqrt{x+2}$,令t=$\sqrt{x+2}$,得到y=t2-t-2,
画出图象,得到k的取值范围为:-$\frac{9}{4}$<k≤-2.
故答案为:-$\frac{9}{4}$<k≤-2
点评 此题考查了进行简单的合情推理,以及函数的值域,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
2.函数f(x)=$\frac{2}{3}$x3-8x在区间[-3,0]上的最大值和最小值分别是( )
| A. | $\frac{32}{3}$,-6 | B. | $\frac{32}{3}$,0 | C. | 6,-$\frac{32}{3}$ | D. | 6,0 |
15.某汽车销售店以8万元/辆的价格购进了某品牌的汽车.根据以往的销售分析得出,当售价定为10万元/辆时,每年可销售100辆该品牌的汽车,当每辆的销售每提高1千元时,年销售量就减少2辆.
(1)若要获利最大年利润,售价应定为多少万元/辆?
(2)该销售店为了提高销售业绩,推出了分期付款的促销活动.已知销售一辆该品牌的汽车,若一次性付款,其利润为2万元;若分2期或3期付款,其利润为2.5万元;若分4期或5期付款,其利润为3万元.该销售店对最近分期付款的10位购车情况进行了统计,统计结果如下表.
若X表示其中任意两辆的利润之差的绝对值,求X的分布列和数学期望.
(1)若要获利最大年利润,售价应定为多少万元/辆?
(2)该销售店为了提高销售业绩,推出了分期付款的促销活动.已知销售一辆该品牌的汽车,若一次性付款,其利润为2万元;若分2期或3期付款,其利润为2.5万元;若分4期或5期付款,其利润为3万元.该销售店对最近分期付款的10位购车情况进行了统计,统计结果如下表.
| 付款方式 | 一次性 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 1 | 1 | 3 | 2 | 3 |
 如图四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,G为MC中点,则下列结论中正确的是①②④.
如图四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,G为MC中点,则下列结论中正确的是①②④. 政府向市民宣传绿色出行(即乘公共汽车、地铁或步行出行),并进行广泛动员,三个月后,统计部门在一个小区随机抽取了100户家庭,调查了他们在政府动员后三个月的月平均绿色出行次数(单位:次),将所得数据分组,画出频率分布直方图(如图所示).
政府向市民宣传绿色出行(即乘公共汽车、地铁或步行出行),并进行广泛动员,三个月后,统计部门在一个小区随机抽取了100户家庭,调查了他们在政府动员后三个月的月平均绿色出行次数(单位:次),将所得数据分组,画出频率分布直方图(如图所示).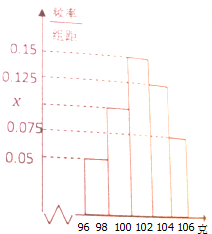 某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).