题目内容
9.已知a∈R,函数f(x)=$\frac{1}{3}{x}^{3}-\frac{1}{2}(a+1){x}^{2}+ax$.(1)求函数f(x)的单调区间;
(2)若a>1,函数y=f(x)在[0,a+1]上最大值是f(a+1),求实数a的取值范围.
分析 (1)由求导公式和法则求出f′(x),求出导函数的零点,然后分a=1,a>1和a<1三种情况,分别由二次函数的性质判断出导数在各区间段内的符号,由导数与函数单调性的关系判断原函数的单调区间;
(2)由(1)和条件判断出f(x)在[0,a+1]上的单调性,确定f(x)在[0,a+1]上的最大值,由条件列出不等式,求出实数a的取值范围.
解答 解:(1)由题意得,f′(x)=x2-(a+1)x+a=(x-1)(x-a),
令f′(x)=0,得x1=1,x2=a,
①当a=1时,f′(x)=(x-1)2≥0,
所以f(x)在(-∞,+∞)单调递增;
②当a<1时,
当x<a或x>1时,f′(x)>0,当a<x<1时,f′(x)<0,
所以f(x)在(-∞,a),(1,+∞)内单调递增,在(a,1)内单调递减;
③当a>1时,
当x<1或x>a时,f′(x)>0,当1<x<a时f′(x)<0,
所以f(x)在(-∞,1),(a,+∞)内单调递增,在(1,a)内单调递减.
综上,当a<1时,f(x)在(-∞,a),(1,+∞)内单调递增,在(a,1)内单调递减;
当a=1时,f(x)在(-∞,+∞)单调递增;
当a>1时,f(x)在(-∞,1),(a,+∞)内单调递增,在(1,a)内单调递减.
(2)由(1)知,当a>1时,
f(x)在(-∞,1),(a,+∞)内单调递增,在(1,a)内单调递减,
所以f(x)在[0,1),(a,a+1]内单调递增,在(1,a)内单调递减,
则f(x)在[0,a+1]上的最大值是f(0)或f(a+1),
因为f(x)在[0,a+1]上最大值是f(a+1),
所以$\left\{\begin{array}{l}{f(a+1)>f(0)}\\{a>1}\end{array}\right.$,则$\left\{\begin{array}{l}{\frac{1}{3}{(a+1)}^{3}-\frac{1}{2}(a+1){(a+1)}^{2}+a(a+1)>0}\\{a>1}\end{array}\right.$,
化简得$\left\{\begin{array}{l}{{a}^{2}-4a+1<0}\\{a>1}\end{array}\right.$,解得$1<a<2+\sqrt{3}$,
所以a的取值范围是(1,2$\sqrt{3}$).
点评 本题考查求导公式、法则,利用导数研究函数的单调性、最值,考查分类讨论思想,是中档题.

| A. | B⊆∁UA | B. | A∩B=∅ | C. | A⊆∁UB | D. | ∁UA∩∁UB=∅ |
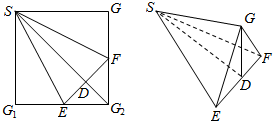 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )| A. | SD⊥平面EFG | B. | SE⊥GF | C. | EF⊥平面SEG | D. | SE⊥SF |
| A. | (-2,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.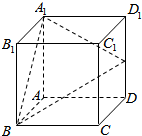 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.