题目内容
14.在以坐标原点为极点,x轴的正半轴为极轴建立的极坐标系中,曲线C1的极坐标方程为ρ=2,正三角形ABC的顶点都在C1上,且A,B,C依逆时针次序排列,点A的坐标为(2,0).(1)求点B,C的直角坐标;
(2)设P是圆C2:x2+(y+$\sqrt{3}$)2=1上的任意一点,求|PB2|+|PC|2的取值范围.
分析 (1)先求出曲线C1的直角坐标方程,由此能求出点B,C的直角坐标.
(2)由圆C2的参数方程结合两点间距离公式,利用三角函数性质能求出|PB2|+|PC|2的取值范围.
解答 解:(1)∵曲线C1的极坐标方程为ρ=2,∴曲线C1的直角坐标方程为x2+y2=4,
∵正三角形ABC的顶点都在C1上,且A,B,C依逆时针次序排列,点A的坐标为(2,0),
∴B点的坐标为(2cos120°,2sin120°),即B(-1,$\sqrt{3}$),
C点的坐标为(2cos240°,2sin240°),即C(-1,-$\sqrt{3}$).
(2)∵圆C2:x2+(y+$\sqrt{3}$)2=1,∴圆C2的参数方程$\left\{\begin{array}{l}{x=cosα}\\{y=-\sqrt{3}+sinα}\end{array}\right.,0≤α<2π$,
设点P(cosα,-$\sqrt{3}+sinα$),0≤α<2π,
∴|PB2|+|PC|2=$(cosα+1)^{2}+(sinα-2\sqrt{3})^{2}$+(cosα+1)2+sin2α
=16+4cosα-4$\sqrt{3}$sinα
=16+8cos($α+\frac{π}{3}$),
∴|PB2|+|PC|2的范围是[8,24].
点评 本题考查点的坐标的求法,考查代数和的取值范围的求法,是基础题,解题时要注意公式参数方程和普通方程的互化和两点间距离公式、三角函数性质的合理运用.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
19.已知双曲线$\frac{x^2}{4}-{y^2}=1$,过点O(0,0)作直线l与双曲线仅有一个公共点,这样的直线l共有( )
| A. | 0条 | B. | 2条 | C. | 4条 | D. | 无数条 |
4.在△ABC中,内角A,B,C对应的边分别为a,b,c,若(a2+b2-c2)tanC=ab,则角C等于( )
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
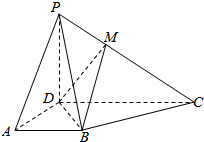 如图所示,已知ABCD为梯形,AB∥CD,CD=2AB,且PD⊥平面ABCD,M为线段PC上一点.
如图所示,已知ABCD为梯形,AB∥CD,CD=2AB,且PD⊥平面ABCD,M为线段PC上一点.