题目内容
8.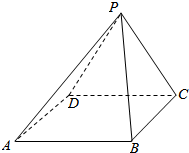 在正四棱锥P-ABCD中,AB=2.
在正四棱锥P-ABCD中,AB=2.(1)若直线PB与底面所成角为$\frac{π}{4}$,求二面角A-PB-C的大小.
(2)若二面角P-BC-D的大小为$\frac{π}{4}$,求面PAD与面PBC所成角的大小,并求点A到PBC的距离.
分析 (1)连结AC,BD,交于点O,连结OP,以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,由直线PB与底面所成角为$\frac{π}{4}$,AB=2,得到PO=BO=$\sqrt{2}$,由此利用向量法能求出二面角A-PB-C的大小.
(2)由二面角P-BC-D的大小为$\frac{π}{4}$,求出OE=PO=1,求出平面PAD的法向量和平面PBC的法向量,由此利用向量法能求出面PAD与面PBC所成角的大小和点A到PBC的距离.
解答 解: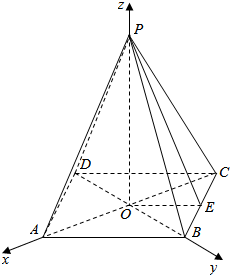 (1)连结AC,BD,交于点O,连结OP,
(1)连结AC,BD,交于点O,连结OP,
∵正四棱锥P-ABCD中,AC⊥BO,
∴以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,
∵直线PB与底面所成角为$\frac{π}{4}$,AB=2,
∴∠PBO=$\frac{π}{4}$,∴PO=BO=$\frac{1}{2}$PB=$\frac{1}{2}\sqrt{4+4}$=$\sqrt{2}$,
∴A($\sqrt{2},0,0$),B(0,$\sqrt{2}$,0),C(-$\sqrt{2}$,0,0),P(0,0,$\sqrt{2}$),
$\overrightarrow{PA}$=($\sqrt{2}$,0,-$\sqrt{2}$),$\overrightarrow{PB}$=(0,$\sqrt{2}$,-$\sqrt{2}$),$\overrightarrow{PC}$=(-$\sqrt{2}$,0,-$\sqrt{2}$),
设平面PAB的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PA}=\sqrt{2}x-\sqrt{2}z=0}\\{\overrightarrow{n}•\overrightarrow{PB}=\sqrt{2}y-\sqrt{2}z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,1,1),
设平面PBC的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PB}=\sqrt{2}b-\sqrt{2}c=0}\\{\overrightarrow{m}•\overrightarrow{PC}=-\sqrt{2}a-\sqrt{2}c=0}\end{array}\right.$,取a=1,得$\overrightarrow{m}$=(1,-1,-1),
设二面角A-PB-C的平面角为α,
则cosα=|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$|=|$\frac{1-1-1}{\sqrt{3}•\sqrt{3}}$|=$\frac{1}{3}$,
∴二面角A-PB-C的大小为arccos$\frac{1}{3}$.
(2)取BC中点E,连结OE,PE,
∵二面角P-BC-D的大小为$\frac{π}{4}$,∴$∠PEO=\frac{π}{4}$,
∵正四棱锥P-ABCD中,AB=2,∴OE=PO=$\frac{1}{2}AB$=1,
A($\sqrt{2}$,0,0),B(0,$\sqrt{2}$,0),C(-$\sqrt{2}$,0,0),D(0,-$\sqrt{2}$,0),P(0,0,1),
$\overrightarrow{PA}$=($\sqrt{2},0,-1$),$\overrightarrow{PB}$=(0,$\sqrt{2}$,-1),
$\overrightarrow{PC}$=($-\sqrt{2},0,-1$),$\overrightarrow{PD}$=(0,-$\sqrt{2}$,-1),
设平面PAD的法向量$\overrightarrow{p}$=(x1,y1,z1),
则$\left\{\begin{array}{l}{\overrightarrow{p}•\overrightarrow{PA}=\sqrt{2}{x}_{1}-{z}_{1}=0}\\{\overrightarrow{p}•\overrightarrow{PD}=-\sqrt{2}{y}_{1}-{z}_{1}=0}\end{array}\right.$,取${x}_{1}=\sqrt{2}$,得$\overrightarrow{p}$=($\sqrt{2}$,-$\sqrt{2}$,2),
设平面PBC的法向量$\overrightarrow{q}=({x}_{2},{y}_{2},{z}_{2})$,
则$\left\{\begin{array}{l}{\overrightarrow{q}•\overrightarrow{PB}=\sqrt{2}{y}_{2}-{z}_{2}=0}\\{\overrightarrow{q}•\overrightarrow{PC}=-\sqrt{2}{x}_{2}-{z}_{2}=0}\end{array}\right.$,取x2=$\sqrt{2}$,得$\overrightarrow{q}$=($\sqrt{2}$,-$\sqrt{2}$,-2)
设面PAD与面PBC所成角的大小为θ,
则cosθ=|cos<$\overrightarrow{p},\overrightarrow{q}$>|=|$\frac{\overrightarrow{p}•\overrightarrow{q}}{|\overrightarrow{p}|•|\overrightarrow{q}|}$|=|$\frac{2+2-4}{\sqrt{8}•\sqrt{8}}$|=0,
∴$θ=\frac{π}{2}$,即面PAD与面PBC所成角的大小为$\frac{π}{2}$.
点A到PBC的距离d=$\frac{|\overrightarrow{PA}•\overrightarrow{q}|}{|\overrightarrow{q}|}$=$\frac{|2+0+2|}{\sqrt{8}}$=$\sqrt{2}$.
∴点A到PBC的距离为$\sqrt{2}$.
点评 本题考查二面角的大小和点到平面的距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | a>7 | B. | 1<a<7 | C. | a>1 | D. | a<7 |
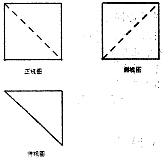 如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )| A. | $\frac{8}{3}$ | B. | $\frac{8}{3}$$\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | 4 |
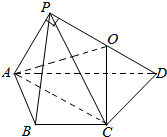 如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点. 如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.
如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.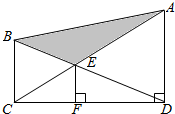 如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.
如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.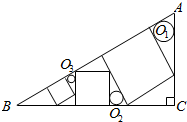 △ABC中,∠C=90°,作三个正方形及三个圆O1,O2,O3,如图,半径分别为r1,r2,r3.证明:r1r3=r${\;}_{2}^{2}$.
△ABC中,∠C=90°,作三个正方形及三个圆O1,O2,O3,如图,半径分别为r1,r2,r3.证明:r1r3=r${\;}_{2}^{2}$.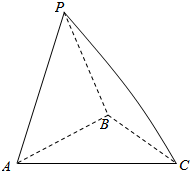 如图所示的三棱锥P-ABC的三条侧棱两两垂直,且PB=1,PA=$\sqrt{3}$,PC=$\sqrt{6}$.
如图所示的三棱锥P-ABC的三条侧棱两两垂直,且PB=1,PA=$\sqrt{3}$,PC=$\sqrt{6}$.