题目内容
已知函数f(x)=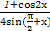 -asin
-asin cos(π-
cos(π- )的最大值为2,则常数a的值为( )
)的最大值为2,则常数a的值为( )
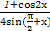 -asin
-asin cos(π-
cos(π- )的最大值为2,则常数a的值为( )
)的最大值为2,则常数a的值为( )A.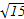 | B.-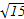 |
C.±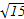 | D.± |
C
【思路点拨】先利用公式进行三角恒等变形,把f(x)化成f(x)=Asin(ωx+φ)的形式,再利用最大值求得a.
解:因为f(x)=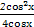 +
+ asinx
asinx
= (cosx+asinx)=
(cosx+asinx)=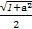 cos(x-φ)(其中tanφ=a),所以
cos(x-φ)(其中tanφ=a),所以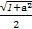 =2,解得a=±
=2,解得a=±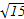 .
.
解:因为f(x)=
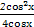 +
+ asinx
asinx=
 (cosx+asinx)=
(cosx+asinx)=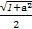 cos(x-φ)(其中tanφ=a),所以
cos(x-φ)(其中tanφ=a),所以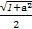 =2,解得a=±
=2,解得a=±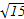 .
.
练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
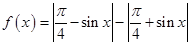 ,则一定在函数
,则一定在函数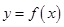 图象上的点是( )
图象上的点是( )



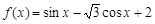 ,记函数
,记函数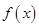 的最小正周期为
的最小正周期为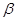 ,向量
,向量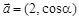 ,
,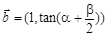 (
(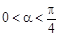 ),且
),且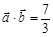 .
.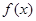 在区间
在区间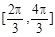 上的最值;
上的最值;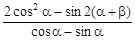 的值.
的值.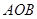 的周长是6,中心角是1弧度,则该扇形的面积为________.
的周长是6,中心角是1弧度,则该扇形的面积为________. 中,已知
中,已知 ,
, 是
是 上一点,
上一点,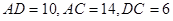 ,则
,则

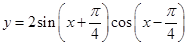 和直线
和直线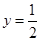 在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3…,则|P2P4|等于______________。
在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3…,则|P2P4|等于______________。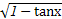 的定义域是 .
的定义域是 .
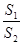 的最小值.
的最小值.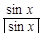 +
+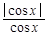 +
+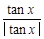 的值域是( )
的值域是( )