题目内容
设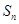 是数列
是数列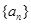 的前
的前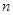 项和,
项和,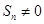 ,
,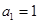 ,
,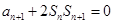 .
.
(1)求证:数列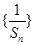 是等差数列,并
是等差数列,并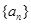 的通项;
的通项;
(2)设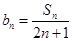 ,求数列
,求数列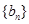 的前
的前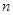 项和
项和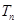 .
.
(1)证明过程详见解析, ;(2)
;(2) .
.
解析试题分析:本题主要考查等差数列的概念、通项公式、数列求和等基础知识,考查化归与转化的思想方法,考查运算能力、推理论证能力.第一问,因为 ,所以变形得
,所以变形得 ,利用等差数列的定义证明,然后直接写出通项公式,再由
,利用等差数列的定义证明,然后直接写出通项公式,再由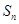 求
求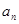 ,注意验证
,注意验证 的情况,第二问,将第一问的结论代入,用裂项相消法求数列的和.
的情况,第二问,将第一问的结论代入,用裂项相消法求数列的和.
试题解析:(Ⅰ)
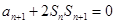 ,∴
,∴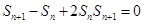 , 2分
, 2分
即 ,
, ,
,
∴数列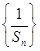 是等差数列. 4分
是等差数列. 4分
由上知数列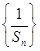 是以2为公差的等差数列,首项为
是以2为公差的等差数列,首项为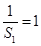 , 5分
, 5分
∴ ,∴
,∴ . 7分
. 7分
∴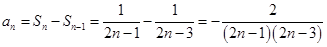 .
.
(或由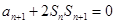 得
得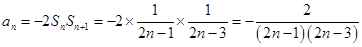 )
)
由题知,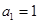
综上,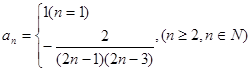 9分
9分
(Ⅱ)由(Ⅰ)知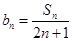
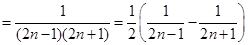 , 10分
, 10分
∴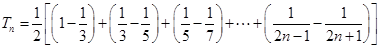 , 12分
, 12分
∴ . 13分
. 13分
考点:1.证明等差数列;2.等差数列的通项公式;3.裂项相消法求和.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 满足:
满足: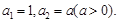 数列
数列 满足
满足 。
。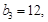 求
求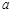 的值及
的值及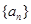 的前
的前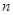 项和为
项和为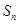 ,公差
,公差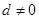 ,且
,且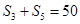 ,
,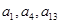 成等比数列.
成等比数列.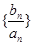 是首项为1公比为3 的等比数列,求数列
是首项为1公比为3 的等比数列,求数列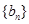 前
前 .
. 是首项是2,公比为q的等比数列,其中
是首项是2,公比为q的等比数列,其中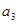 是
是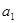 与
与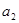 的等差中项.
的等差中项. 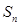
 +
+ +…+
+…+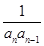 <
<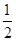 .
.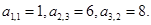

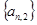 的通项公式;
的通项公式;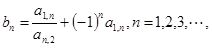 求数列
求数列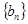 的前
的前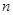 项和
项和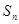 。
。 的首项
的首项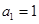 ,公差
,公差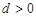 .且
.且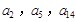 分别是等比数列
分别是等比数列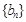 的
的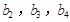 .
. 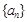 与
与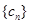 对任意自然数
对任意自然数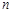 均有
均有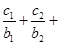
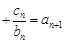 成立,求
成立,求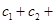
 的值.
的值. 的前
的前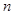 项和为
项和为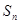 ,已知
,已知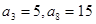 .
. ;
;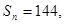 求
求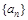 中,
中,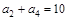 ,
,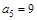 ,数列
,数列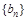 中,
中,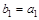 ,
,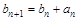 .
.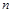 项和
项和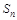 ;
;