题目内容
已知数列 是首项是2,公比为q的等比数列,其中
是首项是2,公比为q的等比数列,其中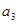 是
是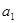 与
与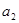 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式. (Ⅱ)求数列
的通项公式. (Ⅱ)求数列 的前n项和
的前n项和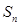
(1)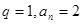
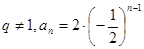
(2) 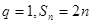

解析试题分析:(Ⅰ)利用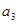 是
是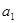 与
与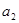 的等差中项,可求出q的值,在分类讨论即可; (Ⅱ)利用(Ⅰ)中求出的数列
的等差中项,可求出q的值,在分类讨论即可; (Ⅱ)利用(Ⅰ)中求出的数列 的通项公式,利用等比数列的前n项和公式即可求出
的通项公式,利用等比数列的前n项和公式即可求出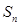 .
.
试题解析:(1)∵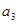 是
是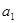 与
与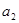 的等差中项 , ∴
的等差中项 , ∴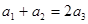 ,又数列
,又数列 是首项是2,公比为q的等比数列,解得
是首项是2,公比为q的等比数列,解得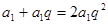 ,∴
,∴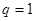 或
或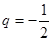 .当
.当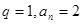 ; 当
; 当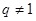 时,
时,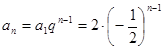 .
.
(2)当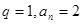 时,
时, 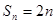 ;当
;当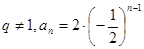 时,
时,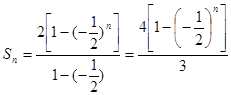 .
.
考点:1.等差中项 ; 2.等比数列的通项公式; 3.等比数列的前n项和公式

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
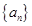 中,
中, 且
且 成等比数列,求数列
成等比数列,求数列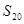 .
.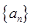 的前
的前 项和为
项和为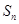 ,
,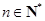 ,且
,且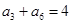 ,
,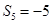 .
.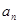 ;
; ,求
,求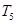 的值和
的值和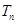 的表达式.
的表达式.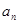 }中,
}中,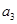 =3,前7项和
=3,前7项和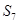 =28。
=28。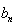 }为等比数列,且
}为等比数列,且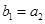 ,
,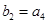 求数列
求数列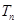
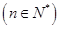 .
.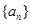 的前
的前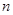 项和为
项和为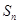 ,
,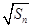 是
是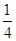 与
与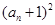 的等比中项.
的等比中项.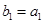 ,且
,且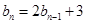 ,求数列
,求数列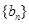 的通项公式;
的通项公式;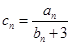 ,求数列
,求数列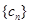 的前
的前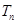 .
.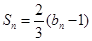 且
且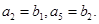
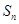 是数列
是数列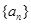 的前
的前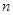 项和,
项和,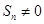 ,
,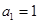 ,
,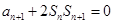 .
.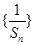 是等差数列,并
是等差数列,并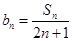 ,求数列
,求数列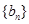 的前
的前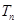 .
.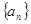 的前
的前 项积为
项积为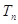 ,且
,且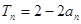
 .
.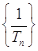 是等差数列;
是等差数列;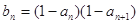 ,求数列
,求数列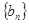 的前
的前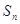 .
.