题目内容
已知定义域为R的函数y=f(x),满足f(2+x)=f(2-x).
(1)求证:函数y=f(x)的图象关于直线x=2对称;
(2)若方程f(x)=0有三个实根,且一个根为0,求另外两根;
(3)若f(x)又是偶函数,且x∈[0,2]时,f(x)=2x-1,求x∈[-4,0]时的f(x)的表达式.
解析:
|
理:(1)p(x0,y0)是y=f(x)的图象上任一点,则y0=f(x0) 点p(x0,y0)关于直线x=2的对称点是 (2) 又f(4)=f(2+2)=f(2-2)=f(0)=0, 设x0是方程的另一个根,则f(X0)=0 由f(x0)=f[2+(x0-2)]=f[2-(x0-2)]=f(4-x0) (3)设x 又f(x+4)=f[2+(2+x)]=f[2-(2+x)]=f(-x)=f(x) 当x f(x)=f(x+4)=2(x+4)-1=2x+7 解:(1)∵对于任意x∈R,都有f(x)-x≥0,且当x∈(0,2)时, 有f(x)≤ ∴1≤f(1)≤ 即f(1)=1. 5分 (2)由a-b+c=0及f(1)=1. 有 又对任意x,f(x)-x≥0,即ax2- ∴a>0且Δ≤0. 即 (3)由(2)可知a>0,c>0. a+c≥2 当且仅当 a=c= ∴f(x)= F(x)=f(x)-mx= 当x∈[-2,2]时,f(x)是单调的,所以F(x)的顶点一定在[-2,2]的外边. ∴ 解得m≤- |

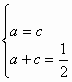 时等号成立.此时
时等号成立.此时