题目内容
4.化下列二次积分为极坐标形式:${∫}_{0}^{1}$dx${∫}_{0}^{1}$f(x,y)dy.分析 根据二重积分为极坐标下的二重积分公式计算即可.
解答 解:${∫}_{0}^{1}$dx${∫}_{0}^{1}$f(x,y)dy=∫∫f(x,y) dxdy 积分区域为矩形:0≤x≤1,0≤y≤1
作y=x将矩形分为两部分分别来做,
x=1对应的极坐标方程为:rcosθ=1,即r=$\frac{1}{cosθ}$,
y=1对应的极坐标方程为:rsinθ=1,即r=$\frac{1}{sinθ}$,
原式=∫∫f(rcosθ,rsinθ)rdrdθ=${∫}_{0}^{\frac{π}{4}}$dθ${∫}_{0}^{\frac{1}{cosθ}}$ f(rcosθ,rsinθ)rdr
+${∫}_{\frac{π}{4}}^{\frac{π}{2}}$dθ${∫}_{0}^{\frac{1}{sinθ}}$ f(rcosθ,rsinθ)rdr.
点评 本题考查了二重积分的极坐标的计算,属于基础题.

练习册系列答案
相关题目
12.如图所示的数阵中,每行、每列的三个数均成等比数列,如果数阵中所有数的乘积等于$\frac{1}{512}$,那么a22=( )
$(\begin{array}{l}{{a}_{11}}&{{a}_{12}}&{{a}_{13}}\\{{a}_{21}}&{{a}_{22}}&{{a}_{23}}\\{{a}_{31}}&{{a}_{32}}&{{a}_{33}}\end{array})$.
$(\begin{array}{l}{{a}_{11}}&{{a}_{12}}&{{a}_{13}}\\{{a}_{21}}&{{a}_{22}}&{{a}_{23}}\\{{a}_{31}}&{{a}_{32}}&{{a}_{33}}\end{array})$.
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
16.已知a∈{1,2,3,4},b∈{1,2,3},则关于x的不等式x2-2(a-1)x+b2≥0的解集为R的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
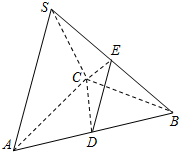 如图,在三棱锥S-ABC中,底面ABC是正三角形,AB=4,SA=SC=2$\sqrt{3}$,侧面SAC⊥底面ABC,D,E分别为AB,SB的中点.
如图,在三棱锥S-ABC中,底面ABC是正三角形,AB=4,SA=SC=2$\sqrt{3}$,侧面SAC⊥底面ABC,D,E分别为AB,SB的中点.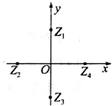 如图,复平面上的点Z1,Z2,Z3,Z4到原点的距离都相等,若复数z所对应的点为Z1,则复数z:i(i是虚数单位)的共轭复数所对应的点为( )
如图,复平面上的点Z1,Z2,Z3,Z4到原点的距离都相等,若复数z所对应的点为Z1,则复数z:i(i是虚数单位)的共轭复数所对应的点为( ) 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论