Question

13．已知在四棱锥S-ABCD中，SA⊥面ABCD，ABCD为正方形，过A且垂直于SC的平面交SB、SC、SD于E、F、G，求证：AE⊥SB．

Answer 1

分析 由SA⊥平面ABCD可得BC⊥SA，正方形ABCD中得BC⊥AB，由线面垂直判定定理证出BC⊥平面SAB，从而得到BC⊥AE．再由SC⊥平面AEFG得到SC⊥AE，从而证出AE⊥平面SBC，可得AE⊥SB．

解答 证明：∵SA⊥平面ABCD，BC?平面ABCD，∴BC⊥SA，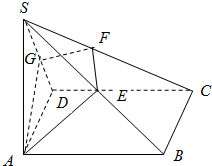
∵四边形ABCD为正方形，∴BC⊥AB，
∵AB、SA是平面SAB内的相交直线，∴BC⊥平面SAB．
∵AE?平面SAB，∴BC⊥AE．
∵SC⊥平面AEFG，AE?平面AEFG，∴SC⊥AE，
∵BC、SC是平面SBC内的相交直线，∴AE⊥平面SBC．
∵SB?平面SBC，∴AE⊥SB．

点评 本题在特殊的四棱锥中证明线线垂直，着重考查了空间线面垂直的判定与性质，及其应用的知识，属于中档题