题目内容
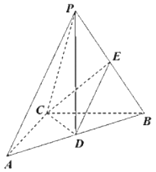
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点;当直线
两点;当直线![]() 经过椭圆
经过椭圆![]() 的下顶点
的下顶点![]() 和右焦点
和右焦点![]() 时,
时,![]() 的周长为
的周长为![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点的横坐标为
的另一个交点的横坐标为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 为
为![]() 内一点,
内一点,![]() 为坐标原点,满足
为坐标原点,满足![]() ,若点
,若点![]() 恰好在圆
恰好在圆![]() 上,求实数
上,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)由椭圆的定义可知,焦点三角形的周长为![]() ,从而求出
,从而求出![]() .写出直线
.写出直线![]() 的方程,与椭圆方程联立,根据交点横坐标为
的方程,与椭圆方程联立,根据交点横坐标为![]() ,求出
,求出![]() 和
和![]() ,从而写出椭圆的方程;
,从而写出椭圆的方程;
(2)设出P、Q两点坐标,由![]() 可知点
可知点![]() 为
为![]() 的重心,根据重心坐标公式可将点
的重心,根据重心坐标公式可将点![]() 用P、Q两点坐标来表示.由点
用P、Q两点坐标来表示.由点![]() 在圆O上,知点M的坐标满足圆O的方程,得
在圆O上,知点M的坐标满足圆O的方程,得![]() 式.
式.![]() 为直线l与椭圆
为直线l与椭圆![]() 的两个交点,用韦达定理表示
的两个交点,用韦达定理表示![]() ,将其代入方程
,将其代入方程![]() ,再利用
,再利用![]() 求得
求得![]() 的范围,最终求出实数
的范围,最终求出实数![]() 的取值范围.
的取值范围.
解:(1)由题意知![]() .
.
![]() ,
,
直线![]() 的方程为
的方程为![]()
∵直线![]() 与椭圆
与椭圆![]() 的另一个交点的横坐标为
的另一个交点的横坐标为![]()

解得![]() 或
或![]() (舍去)
(舍去)
![]() ,
,
∴椭圆![]() 的方程为
的方程为![]()
(2)设![]()
![]() .
.
∴点![]() 为
为![]() 的重心,
的重心,
![]()
∵点![]() 在圆
在圆![]() 上,
上,
![]()
由 得
得 ![]()
![]() ,
,
代入方程![]() ,得
,得
![]() ,
,
即
由![]() 得
得![]()

解得![]() .
.

![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某市一所医院在某时间段为发烧超过38![]() 的病人特设发热门诊,该门诊记录了连续5天昼夜温差
的病人特设发热门诊,该门诊记录了连续5天昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 的资料:
的资料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
昼夜温差 | 8 | 10 | 13 | 12 | 7 |
就诊人数 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并说明昼夜温差(
,并说明昼夜温差(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)求就诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,预测昼夜温差为9
)的线性回归方程,预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
附:样本![]()
![]() 的相关系数为
的相关系数为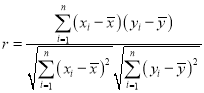 ,当
,当![]() 时认为两个变量有很强的线性相关关系.
时认为两个变量有很强的线性相关关系.
回归直线方程为![]() ,其中
,其中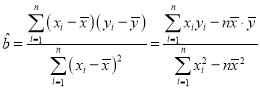 ,
,![]() .
.
参考数据:![]() ,
,![]()