题目内容
【题目】在斜三棱柱![]() 中,
中,![]() 是边长为2的正三角形,侧面
是边长为2的正三角形,侧面![]() 为菱形,且
为菱形,且![]() ,
,![]() ,点O为AC中点.
,点O为AC中点.

(1)求证:![]() 平面ABC;
平面ABC;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接BO,由于侧面![]() 为菱形,
为菱形,![]() ,得
,得![]() ,
,![]() ,由勾股定理得
,由勾股定理得![]() ,
,![]() ,再由线面垂直的判定定理可得证;
,再由线面垂直的判定定理可得证;
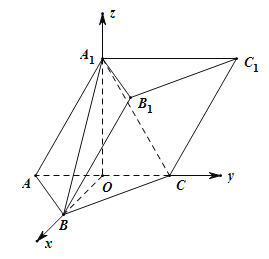
(2)分别以![]() 为x轴,y轴,
为x轴,y轴,![]() 轴的正方向,建立如图所示的空间直角坐标系.由线面角的向量求解方法可求得直线
轴的正方向,建立如图所示的空间直角坐标系.由线面角的向量求解方法可求得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)连接BO,因为侧面![]() 为菱形,
为菱形,![]() ,
,
所以![]() ,因为点O为AC中点,所以
,因为点O为AC中点,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() 是正三角形,
是正三角形,
所以![]() ,且
,且![]()
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() ,
,
![]() 平面ABC,
平面ABC,![]() 平面ABC
平面ABC
所以![]() 平面ABC,
平面ABC,
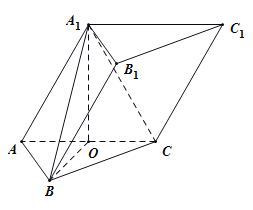
(2)分别以![]() 为x轴,y轴,
为x轴,y轴,![]() 轴的正方向,
轴的正方向,
建立如下图所示的空间直角坐标系.
则![]() ,
,
则![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
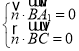 ,即
,即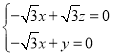 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
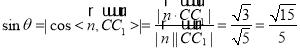 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某种设备随着使用年限的增加,每年的维护费相应增加现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如下表:
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
(1)在这5年中随机抽取两年,求平均每台设备每年的维护费用至少有1年多于2万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程.若该设备的价格是每台16万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?请说明理由.
的线性回归方程.若该设备的价格是每台16万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?请说明理由.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式 .
.