题目内容
(2013•淄博二模)已知函数f(x)=
sinωx•cosωx+cos2ωx-
(ω>0),其最小正周期为
.
(I)求f(x)的表达式;
(II)将函数f(x)的图象向右平移
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间[0,
]上有且只有一个实数解,求实数k的取值范围.
| 3 |
| 1 |
| 2 |
| π |
| 2 |
(I)求f(x)的表达式;
(II)将函数f(x)的图象向右平移
| π |
| 8 |
| π |
| 2 |
分析:(I)利用三角函数的恒等变换化简函数f(x)的表达式为2sin(2ωx+
),再根据它的最小正周期为
,求得ω=2,从而求得f(x)的表达式.
(Ⅱ)根据函数y=Asin(ωx+∅)的图象变换规律,可得g(x)=sin(2x-
),由题意可得函数y=g(x)与y=k在区间[0,
]上有且只有一个交点,结合正弦函数的图象求得实数k的取值范围.
| π |
| 6 |
| π |
| 2 |
(Ⅱ)根据函数y=Asin(ωx+∅)的图象变换规律,可得g(x)=sin(2x-
| π |
| 3 |
| π |
| 2 |
解答:解:(I)f(x)=
sinωx•cosωx+cos2ωx-
=
sin2ωx+
-
=sin(2ωx+
).…(3分)
由题意知f(x)的最小正周期T=
,T=
=
=
,所以ω=2…(5分)
所以,f(x)=sin(4x+
)…(6分)
(Ⅱ)将f(x)的图象向右平移个
个单位后,得到y=sin(4x-
)的图象,
再将所得图象所有点的横坐标伸长到原来的2倍,纵坐标不变,得到y=sin(2x-
)的图象.
所以g(x)=sin(2x-
)…(9分)
因为0≤x≤
,所以-
≤2x-
≤
.
g(x)+k=0 在区间[0,
]上有且只有一个实数解,即函数y=g(x)与y=k在区间[0,
]上有且只有一个交点,
由正弦函数的图象可知-
≤-k<
,或k=-1,
所以-
<k≤
,或k=-1.…(12分)
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| cos2ωx+1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
由题意知f(x)的最小正周期T=
| π |
| 2 |
| 2π |
| 2ω |
| π |
| ω |
| π |
| 2 |
所以,f(x)=sin(4x+
| π |
| 6 |
(Ⅱ)将f(x)的图象向右平移个
| π |
| 8 |
| π |
| 3 |
再将所得图象所有点的横坐标伸长到原来的2倍,纵坐标不变,得到y=sin(2x-
| π |
| 3 |
所以g(x)=sin(2x-
| π |
| 3 |
因为0≤x≤
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
g(x)+k=0 在区间[0,
| π |
| 2 |
| π |
| 2 |
由正弦函数的图象可知-
| ||
| 2 |
| ||
| 2 |
所以-
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查三角函数的恒等变换及化简求值,y=Asin(ωx+∅)的图象变换规律,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
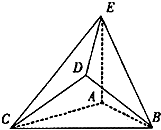 (2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
(2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD. (2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=
(2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=