题目内容
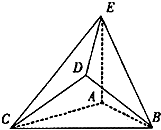 (2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
(2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.(Ⅰ)AE∥平面BCD;
(Ⅱ)平面BDE⊥平面CDE.
分析:(Ⅰ)取BC的中点M,连接DM、AM,证明DM⊥平面ABC,再由AE⊥平面ABC,可得AE∥DM,从而得AE∥平面BCD.
(Ⅱ)由(Ⅰ)可得DMAE是平行四边形,故有DE∥AM,再由AM⊥平面BCD证得DE⊥平面BCD.
(Ⅱ)由(Ⅰ)可得DMAE是平行四边形,故有DE∥AM,再由AM⊥平面BCD证得DE⊥平面BCD.
解答: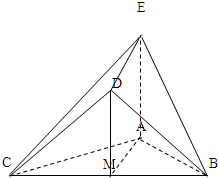 证明:(Ⅰ) 取BC的中点M,连接DM、AM,由已知可得DM=1,DM⊥BC,AM⊥BC.
证明:(Ⅰ) 取BC的中点M,连接DM、AM,由已知可得DM=1,DM⊥BC,AM⊥BC.
又因为平面BCD⊥平面ABC,所以DM⊥平面ABC.…(2分)
因为AE⊥平面ABC,所以,AE∥DM.…(4分)
又因为AE?平面BCD,DM?平面BCD,所以AE∥平面BCD.…(6分)
(Ⅱ)由(Ⅰ)知AE∥DM,又AE=1,DM=1,
所以四边形DMAE是平行四边形,则有DE∥AM.
因为AM⊥平面BCD,所以DE⊥平面BCD.…(8分)
又CD?平面BCD,所以DE⊥CD.
由已知BD⊥CD,则CD⊥平面BDE.…(10分)
因为CD?平面CDE,所以,平面BDE⊥平面CDE.…(12分)
 证明:(Ⅰ) 取BC的中点M,连接DM、AM,由已知可得DM=1,DM⊥BC,AM⊥BC.
证明:(Ⅰ) 取BC的中点M,连接DM、AM,由已知可得DM=1,DM⊥BC,AM⊥BC.又因为平面BCD⊥平面ABC,所以DM⊥平面ABC.…(2分)
因为AE⊥平面ABC,所以,AE∥DM.…(4分)
又因为AE?平面BCD,DM?平面BCD,所以AE∥平面BCD.…(6分)
(Ⅱ)由(Ⅰ)知AE∥DM,又AE=1,DM=1,
所以四边形DMAE是平行四边形,则有DE∥AM.
因为AM⊥平面BCD,所以DE⊥平面BCD.…(8分)
又CD?平面BCD,所以DE⊥CD.
由已知BD⊥CD,则CD⊥平面BDE.…(10分)
因为CD?平面CDE,所以,平面BDE⊥平面CDE.…(12分)
点评:本题主要考查直线和平面平行的判定定理的应用,直线和平面垂直,平面和平面垂直的判定定理的应用,取BC的中点M,连接DM、AM,是解题的突破口,属于中档题.

练习册系列答案
相关题目
 (2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=
(2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=