题目内容
（2013•淄博二模）集合A={-1，0，1}，B={y|y=ex，x∈A}，则A∩B=（ ）
分析：集合B中的自变量属于集合A，把集合A中的元素代入函数求出值域，确定出集合B，找出两集合的公共部分，即可确定出两集合的交集．
解答：解：∵y=ex，x∈A
∴当x=-1时，y=
，当x=1时，y=e，当x=0时，y=1．
∴可知B={
，e，1}，
又集合A={-1，0，1}，
则A∩B={1}．
故选B．
∴当x=-1时，y=
| 1 |
| e |
∴可知B={
| 1 |
| e |
又集合A={-1，0，1}，
则A∩B={1}．
故选B．
点评：本题主要考查了函数值域为平台，考查了交集的运算，是一道基础题．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
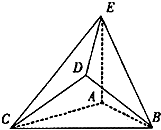（2013•淄博二模）在如图所示的几何体中，△ABC是边长为2的正三角形，AE=1，AE⊥平面ABC，平面BCD⊥平面ABC，BD=CD，且BD⊥CD．
（2013•淄博二模）如图，平行四边形ABCD中，AB=2，AD=1，∠A=60°，点M在AB边上，且AM=