题目内容
设a,b为正实数.现有下列命题:
①若a2-b2=1,则a-b<1; ②若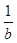 -
-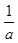 =1,则a-b<1;
=1,则a-b<1;
③若|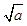 -
-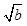 |=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.
|=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.
其中真命题有 .(写出所有真命题的编号)
①若a2-b2=1,则a-b<1; ②若
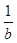 -
-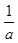 =1,则a-b<1;
=1,则a-b<1;③若|
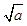 -
-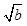 |=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.
|=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.其中真命题有 .(写出所有真命题的编号)
①④
试题分析:对于①,因为
 ,由此可知
,由此可知 ,若
,若 这与
这与 矛盾,故有
矛盾,故有 成立,所以①为真;对于②取
成立,所以①为真;对于②取 知
知 ,所以②不真;对于③取
,所以②不真;对于③取 成立,但
成立,但 不成立,所以③不真;对于④由
不成立,所以③不真;对于④由 得到:
得到: ,又因为
,又因为 中至少有一个大于1(否则已知|a3-b3|=1不成立),从而
中至少有一个大于1(否则已知|a3-b3|=1不成立),从而 成立,故④为真;综上可知真命题有①④.
成立,故④为真;综上可知真命题有①④.
练习册系列答案
相关题目
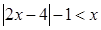 .
.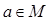 ,求证:
,求证: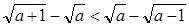
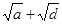 <
< 
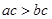 ,则
,则
 ,则
,则 ,则
,则
 ,则
,则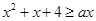 ,对于一切的
,对于一切的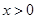 恒成立,则
恒成立,则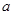 的取值范围是_________。
的取值范围是_________。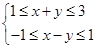 ,则
,则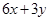 的取值范围是________.
的取值范围是________. 的两个不等实根都大于2,则实数k的取值范围是()
的两个不等实根都大于2,则实数k的取值范围是()