题目内容
9.若1+$\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}}>\frac{127}{64},n∈{N}^{*}$,则n的最小值为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 利用求和公式可将原不等式化简为$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$>$\frac{127}{64}$,进而计算可得结论.
解答 解:∵1+$\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}}>\frac{127}{64},n∈{N}^{*}$,
∴$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$>$\frac{127}{64}$,
整理得:$\frac{1}{{2}^{n-1}}$<$\frac{1}{64}$,
解得:n>7,
故选:C.
点评 本题考查数列的求和,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
20.一枚质地均匀的正四面体玩具,有三个面标有数字1,一个面标有数字2,抛掷两次,所得向上数字相同的概率是( )
| A. | $\frac{3}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | 不同于以上答案 |
4.三个数50.6,0.65,log0.65的大小顺序是( )
| A. | 0.65<log0.65<50.6 | B. | 0.65<50.6<log0.65 | ||
| C. | log0.65<0.65<50.6 | D. | log0.65<50.6<0.65 |
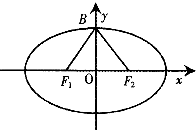 设F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点,B为短轴的一个端点,且△F1BF2是边长为2的等边三角形.
设F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点,B为短轴的一个端点,且△F1BF2是边长为2的等边三角形.