题目内容
1．100件产品中有97件合格品，3件次品，从中任意取5件进行检查，问：（1）抽取5件都是合格品的抽法有多少种？
（2）抽出的5件中恰好有2件是次品的抽法有多少种？
（3）抽出的5件至少有2件是次品的抽法有多少种？
分析 （1）抽出的5件产品都是合格品，即从97件合格品抽取5件；
（2）抽出的5件产品中恰好有2件是次品，即从3件次品抽取2件，97件合格品抽取3件；
（3））抽出的5件至少有2件包括恰好有2件是次品、恰好有3件是次品．
解答 解：（1）抽取5件都是合格品的抽法有C975种；
（2）抽出的5件中恰好有2件是次品的抽法有C32C973种；
（3）抽出的5件至少有2件是次品的抽法有C32C973+C33C972种．
点评 本题考查组合知识的运用，考查学生利用数学知识解决实际问题的能力，属于中档题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
11．函数f（x）=$\frac{1}{3}$x3+x在点处（1，$\frac{4}{3}$）的切线与坐标轴围成的三角形的面积为（ ）
| A． | 3 | B． | $\frac{1}{3}$ | C． | 2 | D． | $\frac{1}{9}$ |
9．若1+$\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}}＞\frac{127}{64}，n∈{N}^{*}$，则n的最小值为（ ）
| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
16．
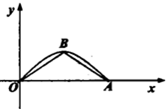如图是函数f（x）=sinx（x∈[0，π]）的图象，其中B为顶点，若在f（x）的图象与x轴所围成的区域内任意投进一个点P，则点P落在△OAB内的概率为（ ）
如图是函数f（x）=sinx（x∈[0，π]）的图象，其中B为顶点，若在f（x）的图象与x轴所围成的区域内任意投进一个点P，则点P落在△OAB内的概率为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
6．已知正三棱柱ABC-A1B1C1（侧棱AA1⊥底面A1B1C1，底面△A1B1C1是正三角形）内接于球O，AB1与底面A1B1C1所成的角是45°，若正三棱柱ABC-A1B1C1的体积是2$\sqrt{3}$cm3，则球O的表面积是（ ）
| A． | $\frac{28π}{3}$cm2 | B． | $\frac{14π}{3}$cm2 | C． | $\frac{56π}{3}$cm2 | D． | $\frac{7π}{3}$cm2 |
10．已知数列{an}的前n项和为Sn，a1=1，Sn=2an+1，则a10=（ ）
| A． | $\frac{{3}^{7}}{{2}^{8}}$ | B． | $\frac{{3}^{7}}{{2}^{9}}$ | C． | $\frac{{3}^{8}}{{2}^{8}}$ | D． | $\frac{{3}^{8}}{{2}^{9}}$ |