题目内容
13.已知函数f(x)=ln$\frac{1+x}{1-x}$.(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求证:当x∈(0,1)时,f(x)>2(x+$\frac{{x}^{3}}{3}$)
分析 (1)求得函数的导数,求得切线的斜率和切点坐标,即可得到所求切线的方程;
(2)构造函数y=ln$\frac{1+x}{1-x}$-2(x+$\frac{{x}^{3}}{3}$),0<x<1,求得导数,判断符号,由单调性即可得证.
解答 (1)解:f(x)=ln$\frac{1+x}{1-x}$的导数为
f′(x)=$\frac{1-x}{1+x}$•$\frac{2}{(x-1)^{2}}$=-$\frac{2}{{x}^{2}-1}$,
可得在点(0,f(0))处的切线斜率为2,切点(0,0),
即有在点(0,f(0))处的切线方程为y=2x;
(2)证明:由y=ln$\frac{1+x}{1-x}$-2(x+$\frac{{x}^{3}}{3}$),0<x<1,
导数为y′=$\frac{1-x}{1+x}$•$\frac{2}{(1-x)^{2}}$-2(1+x2)
=$\frac{2}{1-{x}^{2}}$-2(1+x2)=$\frac{2{x}^{4}}{1-{x}^{2}}$,
由0<x<1可得$\frac{2{x}^{4}}{1-{x}^{2}}$>0,
即导数y′>0在(0,1)恒成立,
则有函数y=ln$\frac{1+x}{1-x}$-2(x+$\frac{{x}^{3}}{3}$)在(0,1)递增,
则有ln$\frac{1+x}{1-x}$-2(x+$\frac{{x}^{3}}{3}$)>0,
故有当x∈(0,1)时,f(x)>2(x+$\frac{{x}^{3}}{3}$).
点评 本题考查导数的运用:求切线的方程和单调区间,考查不等式的证明,注意运用单调性,属于中档题.

练习册系列答案
相关题目
2.下列对应是从集合S到T的映射的是( )
| A. | S={0,1,4,9},T={-3,-2,-1,0,1,2,3},对应法则是开平方 | |
| B. | S={0,1,2,5},T=$\{1,\frac{1}{2},\frac{1}{5}\}$,对应法则是取倒数 | |
| C. | S=N,T={-1,1},对应法则是n→(-1)n,n∈S | |
| D. | S={x|x∈R},T={y|y∈R},对应法则是x→y=$\frac{1+x}{1-x}$ |
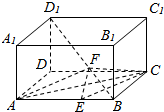 如图,在长方体ABCD-A1B1C1D1中,AB=3,AA1=AD=2,BE=1,F是BD1上一点,且EF∥平面ADD1A1,则三棱锥E-AFC的体积为$\frac{4}{9}$.
如图,在长方体ABCD-A1B1C1D1中,AB=3,AA1=AD=2,BE=1,F是BD1上一点,且EF∥平面ADD1A1,则三棱锥E-AFC的体积为$\frac{4}{9}$. 直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?
直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?