题目内容
1．在△ABC中，a=80，b=100，A=30°，则B的解的个数是2个．分析 由条件利用正弦定理求得sinB=$\frac{5}{8}$＞sinA，可得 B=arcsin$\frac{5}{8}$，或 B=π-arcsin$\frac{5}{8}$，可得△ABC有两解．
解答 解：△ABC中，∵a=80，b=100，A=30°，则由正弦定理可得 $\frac{a}{sinA}$=$\frac{b}{sinB}$，即$\frac{80}{\frac{1}{2}}$=$\frac{100}{sinB}$，
求得sinB=$\frac{5}{8}$＞sinA，∴B=arcsin$\frac{5}{8}$，或 B=π-arcsin$\frac{5}{8}$，故△ABC有两解，
故答案为：2个．
点评 本题主要考查利用正弦定理求三角形的解的个数，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，边长为2的正方体ABCD-A1B1C1D1中，B1C与BC1相交于点O．
如图，己知L、K分别是△ABC的边AB、AC的中点．△ABC的内切圆⊙l分别与边BC、CA切于点D、E．求证：KL、DE的交点在∠ABC的角平分线上．
16．
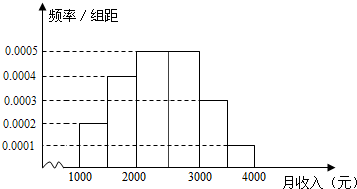某市统计局就某地居民的月收入调查了10 000人，并根据所得数据画出样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在[1 000，1 500）内）．根据频率分布直方图算出样本数据的中位数是（ ）
某市统计局就某地居民的月收入调查了10 000人，并根据所得数据画出样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在[1 000，1 500）内）．根据频率分布直方图算出样本数据的中位数是（ ）| A． | 2360 | B． | 2380 | C． | 2400 | D． | 2420 |
6．圆C1：（x-1）2+（y-1）2=1关于直线x+y=0对称的圆C2的方程为（ ）
| A． | （x+1）2+（y-1）2=1 | B． | （x-1）2+（y+1）2=1 | ||
| C． | （x+1）2+（y+1）2=1 | D． | （x+1）2+（y-1）2=1或（x-1）2+（y+1）2=1 |