题目内容
.本小题满分12分)已知函数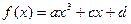
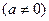 是R上的奇函数,
是R上的奇函数,
当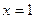 时
时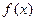 取得极值
取得极值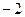 ,
,
(1)求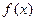 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意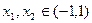 ,不等式
,不等式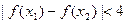 恒成立. 、
恒成立. 、
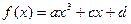
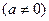 是R上的奇函数,
是R上的奇函数,当
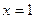 时
时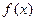 取得极值
取得极值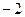 ,
,(1)求
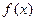 的单调区间和极大值;
的单调区间和极大值;(2)证明对任意
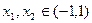 ,不等式
,不等式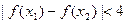 恒成立. 、
恒成立. 、解:∵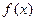 为R上的奇函数,∴
为R上的奇函数,∴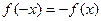 ,
,
即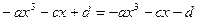 ,∴d=0.∴
,∴d=0.∴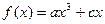 ,
,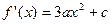 .
.
∵当x=1时,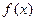 取得极值
取得极值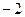 .∴
.∴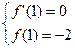 ∴
∴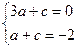 解得:
解得: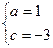 .
.
∴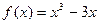 ,
,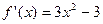 ,
,
令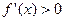 ,则
,则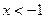 或
或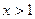 ,令
,令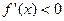 ,则
,则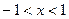 .
.
∴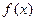 的单调递增区间为
的单调递增区间为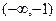 和
和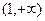 ,单调递减区间为
,单调递减区间为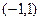 .…………6分
.…………6分
(2)证明:由(1)知,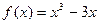 ,(
,(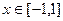 )是减函数,
)是减函数,
且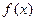 在
在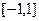 上的最大值
上的最大值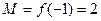 ,
,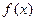 在
在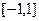 上的最小值
上的最小值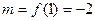 ,
,
∴对任意的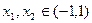 ,恒有
,恒有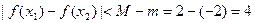 …………12分
…………12分
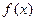 为R上的奇函数,∴
为R上的奇函数,∴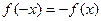 ,
,即
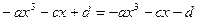 ,∴d=0.∴
,∴d=0.∴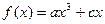 ,
,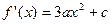 .
.∵当x=1时,
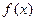 取得极值
取得极值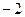 .∴
.∴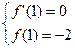 ∴
∴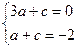 解得:
解得: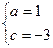 .
.∴
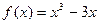 ,
,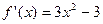 ,
,令
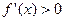 ,则
,则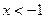 或
或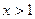 ,令
,令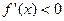 ,则
,则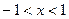 .
.∴
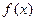 的单调递增区间为
的单调递增区间为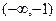 和
和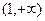 ,单调递减区间为
,单调递减区间为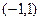 .…………6分
.…………6分(2)证明:由(1)知,
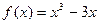 ,(
,(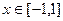 )是减函数,
)是减函数,且
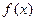 在
在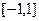 上的最大值
上的最大值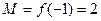 ,
,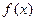 在
在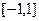 上的最小值
上的最小值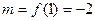 ,
,∴对任意的
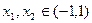 ,恒有
,恒有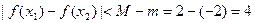 …………12分
…………12分略

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
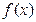 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: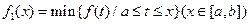 ,
,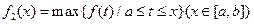 ,其中
,其中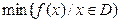 表示函数
表示函数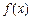 在D上的最小值,
在D上的最小值,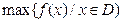 表示函数
表示函数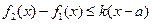 对任意的
对任意的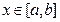 成立,则称函数
成立,则称函数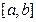 上的“k阶收缩函数”
上的“k阶收缩函数”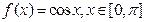 ,试写出
,试写出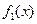 ,
,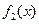 的表达式;
的表达式;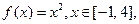 试判断
试判断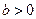 ,函数
,函数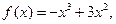 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围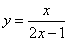 在点
在点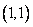 处的切线方程为____________。
处的切线方程为____________。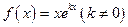
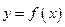 在点
在点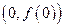 处的切线方程。
处的切线方程。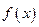 在区间
在区间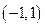 内单调递增,求
内单调递增,求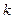 的取值范围。
的取值范围。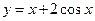 在区间
在区间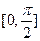 上的最大值是
上的最大值是 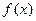 的定义域为开区间
的定义域为开区间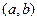 ,导函数
,导函数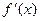 在
在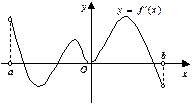

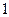 个 B
个 B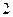 个 C
个 C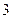 个 D
个 D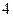 个
个 一个对称图形做的薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻该薄片露出水面部分的图形面积为
一个对称图形做的薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻该薄片露出水面部分的图形面积为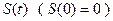 ,那么导函数
,那么导函数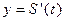 的图像大致为
的图像大致为

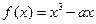 在区间
在区间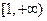 上是单调增函数,则
上是单调增函数,则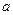 的最大值为 ( )
的最大值为 ( )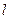 与曲线
与曲线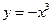 相切于点A(-1,1),则切线的方程是
相切于点A(-1,1),则切线的方程是